Matemática
Exibindo questões de 301 a 400.
Lúcia está usando as jarras vazias 1 e 2, ambas de - FGV 2019
Matemática - 2019Lúcia está usando as jarras vazias 1 e 2, ambas de capacidade 800 mL cada, para fazer uma mistura de café com leite. Inicialmente, ela coloca 400 mL de café na jarra 1 e 400 mL de leite na jarra 2. Em seguida, ela transfere a metade do conteúdo da jarra 1 para a jarra 2. Ela mexe com a colher até que a mistura de café e leite fique homogênea e, em seguida, transfere metade desse conteúdo para a jarra 1.
O texto a seguir refere-se aos dados do PIB e do PIB per - FGV 2019
Matemática - 2019O texto a seguir refere-se aos dados do PIB e do PIB per capita do Brasil, comparando os anos de 2016 e 2017.

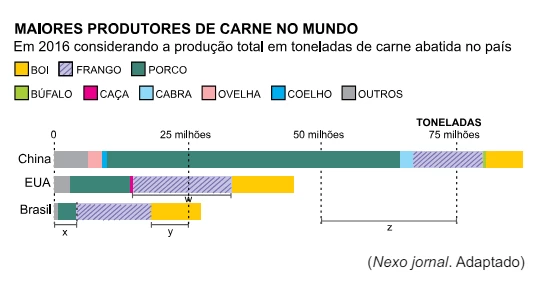
No infográfico, indicado a seguir, x, y, z e w representam - FGV 2019
Matemática - 2019No infográfico, indicado a seguir, x, y, z e w representam comprimentos em uma mesma unidade de medida. Considere que o infográfico esteja em escala.
Existem dois valores distintos para a média aritmética dos - FGV 2019
Matemática - 2019Existem dois valores distintos para a média aritmética dos números reais representados por F, G e V, de maneira que a sequência (–3, F, G, V, –768) seja geométrica.
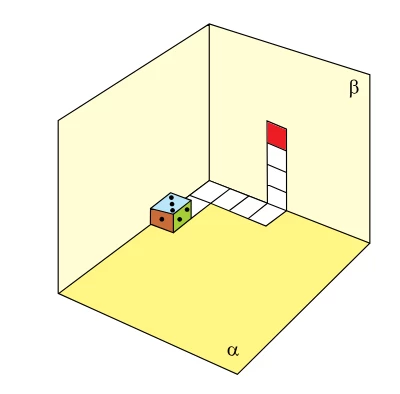
Um dado convencional possui a soma dos números de faces - FGV 2019
Matemática - 2019Um dado convencional possui a soma dos números de faces opostas sempre igual a 7. A situação descrita na figura indica um dado convencional que irá rolar por um caminho demarcado no chão (plano α), e, em seguida, pelo caminho demarcado na parede de uma sala (plano β). O percurso do dado encerra-se quando ele chega no quadrado vermelho.
Quando um cliente efetua uma compra com o cartão de crédito - FGV 2019
Matemática - 2019Quando um cliente efetua uma compra com o cartão de crédito, o estabelecimento comercial que realizou a venda paga 5% do valor da compra para a operadora da máquina eletrônica. Se a mesma compra for feita com pagamento pelo cartão de débito, o comerciante paga 2% para a operadora da máquina. Se o preço de venda de um produto é igual a p reais, esse mesmo produto poderia ser vendido pelo comerciante por q reais se o pagamento fosse por cartão de débito, sem perda nem lucro para ele na comparação com o pagamento feito por cartão de crédito.
Existem dois valores reais de m que fazem com que a reta de - FGV 2019
Matemática - 2019Existem dois valores reais de m que fazem com que a reta de equação y = mx + 3 tangencie a parábola de equação y = 0,5x2 – x + 5.
Os números reais x, y e z são tais que 101x + 303y = 505 e - FGV 2019
Matemática - 2019Os números reais x, y e z são tais que 101x + 303y = 505 e 101z – 202y = 404.
A parábola de equação y = x2 + 5x + 8, quando refletida em - FGV 2019
Matemática - 2019A parábola de equação y = x2 + 5x + 8, quando refletida em relação à reta de equação y = x,
Um cilindro circular reto de altura igual ao diâmetro da - FGV 2019
Matemática - 2019Um cilindro circular reto de altura igual ao diâmetro da base está inscrito em um cone circular reto. O cone tem diâmetro 10, altura 12 e seu eixo de revolução coincide com o do cilindro.
Se o produto 2564 . 6425 é igual ao quadrado de um número - FGV 2019
Matemática - 2019Se o produto 2564 . 6425 é igual ao quadrado de um número inteiro positivo x,
O conjunto solução do sistema de inequações modulares dado - FGV 2019
Matemática - 2019O conjunto solução do sistema de inequações modulares dado por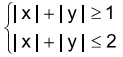
Dadas as matrizes quadradas e A = e B = , o valor de é igua - FGV 2019
Matemática - 2019Dadas as matrizes quadradas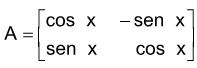 E
E 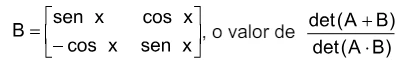
O paralelogramo ABCD, indicado na figura, é tal que - FGV 2019
Matemática - 2019O paralelogramo ABCD, indicado na figura, é tal que BE = BC/4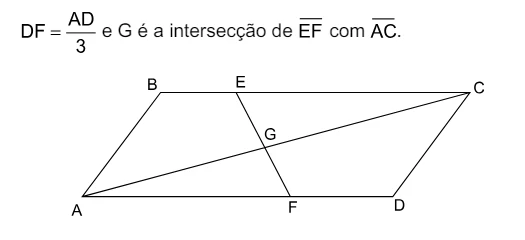
Uma caixa contém duas bolas pretas e três bolas brancas. As - FGV 2019
Matemática - 2019Uma caixa contém duas bolas pretas e três bolas brancas. As bolas são removidas aleatoriamente da caixa, uma a uma e sem reposição, até que todas as bolas brancas sejam removidas ou até que todas as bolas pretas sejam removidas.
A respeito do sistema de equações lineares, nas incógnitas - FGV 2018
Matemática - 2019A respeito do sistema de equações lineares, nas incógnitas x e y, dado por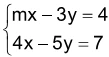
Sem o uso de balança, pequenos produtores de gado estimam o - FGV 2019
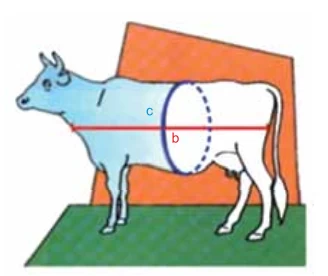
Matemática - 2019Sem o uso de balança, pequenos produtores de gado estimam o “peso” (P), em kg, de um boi medindo o comprimento da cintura (c), em dm, e o comprimento do tronco (b), em dm, do boi. A fórmula usada na estimativa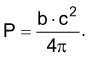
Clara ganhou R$ 20,00 em uma raspadinha. Mateus, seu - FGV 2019
Matemática - 2019Clara ganhou R$ 20,00 em uma raspadinha. Mateus, seu namorado, sugeriu que ela dividisse o prêmio com ele. Clara disse que daria y reais para Mateus, com y sendo a soma das soluções reais não negativas da equação (x2 – 17)5x–2 = 1, se ele resolvesse corretamente essa equação em R.
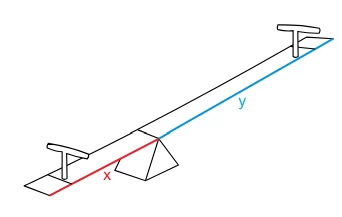
A figura indica uma gangorra apoiada no chão plano. As - FGV 2019
Matemática - 2019A figura indica uma gangorra apoiada no chão plano. As medidas x e y estão em centímetros, sendo que y é maior do que x. Quando encostada com o chão de um dos lados, a gangorra forma ângulo de 50°. Do outro lado, quando encostada com o chão, a gangorra forma ângulo de 40° com ele.
A equação = possui três raízes em C, sendo que a) uma delas - FGV 2019
Matemática - 2019A equação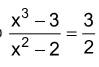
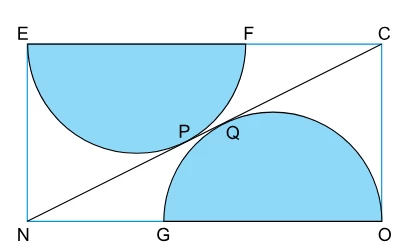
A figura indica um retângulo ECON, com F e G pertencentes a - FGV 2019
Matemática - 2019A figura indica um retângulo ECON, com F e G pertencentes a EC e NO. Os semicírculos indicados possuem diâmetros EF e GO, além de tangenciarem a diagonal CN de ECON em P e Q.
O conjunto solução de –1 < tg x < 1, com x ∈ [0, π ], é: - FGV 2019
Matemática - 2019O conjunto solução de
Em uma máquina fotográfica, a abertura na lente, pela qual - FGV 2018
Matemática - 2019Em uma máquina fotográfica, a abertura na lente, pela qual passa a luz, é indicada pela letra f. Admita que a fórmula que fornece a medida da luz (S) que passa pela abertura, em função do valor de f, para uma câmera de lente 35 mm, seja dada por S = log2 f2.

Uma prova contém 60 testes de múltipla escolha, cada um com - FGV 2019
Matemática - 2019Uma prova contém 60 testes de múltipla escolha, cada um com 4 alternativas das quais apenas uma é correta. Catarina tem 40% de chances de resolver corretamente cada teste. Quando não sabe resolver um teste, ela assinala aleatoriamente uma das 4 alternativas.
O coeficiente angular (m) da reta tangente à parábola de - FGV 2019
Matemática - 2019O coeficiente angular (m) da reta tangente à parábola de equação y = ax2m + bx + c no ponto (x0, y0) é dado por m = 2ax0 + b. Nas condições descritas,
Uma porta eletrônica possui 6 botões. As digitações dos - FGV 2019
Matemática - 2019Uma porta eletrônica possui 6 botões. As digitações dos botões que podem ser usadas para programar o sistema de abertura da porta são:
• todas sequências de 5 digitações, sem que se repita um botão digitado;
• todas as possibilidades em que são digitados dois botões, simultaneamente, e, em seguida, três botões, simultaneamente, podendo repetir os botões;
• todas as possibilidades em que são digitados três botões, simultaneamente, e, em seguida, dois botões, simultaneamente, sem poder repetir os botões.
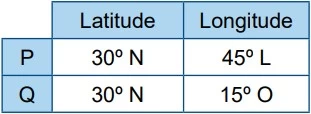
Os pontos P e Q sobre a superfície da Terra possuem as - UNESP 2019
Matemática - 2019Os pontos P e Q sobre a superfície da Terra possuem as seguintes coordenadas geográficas:
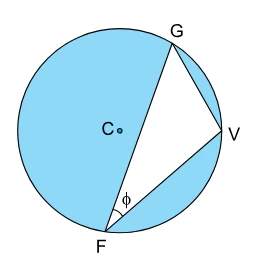
O triângulo FGV indicado na figura está inscrito em uma - FGV 2019
Matemática - 2019O triângulo FGV indicado na figura está inscrito em uma circunferência de centro C.
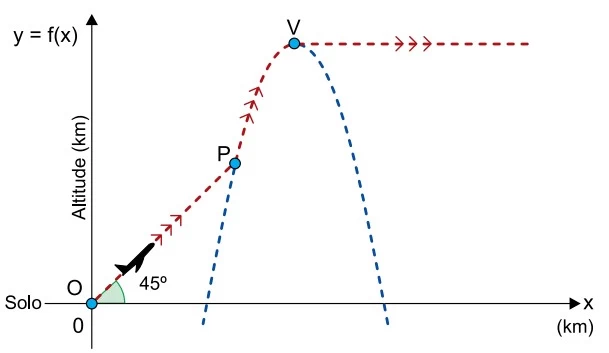
Em relação a um sistema cartesiano de eixos ortogonais - UNESP 2019
Matemática - 2019Em relação a um sistema cartesiano de eixos ortogonais com origem em O(0, 0), um avião se desloca, em linha reta, de O até o ponto P, mantendo sempre um ângulo de inclinação de 45º com a horizontal. A partir de P, o avião inicia trajetória parabólica, dada pela função f(x) = –x2 + 14x – 40, com x e f(x) em quilômetros. Ao atingir o ponto mais alto da trajetória parabólica, no ponto V, o avião passa a se deslocar com altitude constante em relação ao solo, representado na figura pelo eixo x.
A tabuleiro indicado na figura contém 36 casas, cada uma - FGV 2019
Matemática - 2019A tabuleiro indicado na figura contém 36 casas, cada uma marcada com um número diferente. Sobre as casas marcadas com os números 55 e 103, foram colocadas duas fichas azuis.
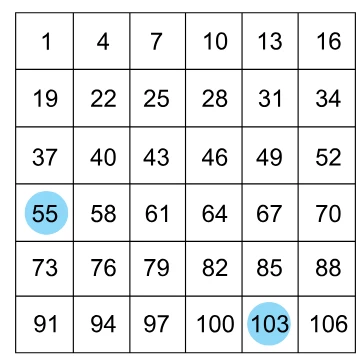
Outras quatro fichas devem ser colocadas sobre outras quatro casas do tabuleiro de tal forma que, na configuração final com seis fichas, não haja duas ou mais fichas em uma mesma coluna, em uma mesma linha e em uma mesma diagonal.
Dois números reais de 0 a 4, e que podem ser iguais - UNESP 2019
Matemática - 2019Dois números reais de 0 a 4, e que podem ser iguais, serão sorteados ao acaso.
Em um dia de aula, faltaram 3 alunas e 2 alunos porque - UNESP 2019
Matemática - 2019Em um dia de aula, faltaram 3 alunas e 2 alunos porque os cinco estavam gripados. Dos alunos e alunas que foram à aula, 2 meninos e 1 menina também estavam gripados. Dentre os meninos presentes à aula, a porcentagem dos que estavam gripados era 8% e, dentre as meninas, a porcentagem das que estavam gripadas era 5%.
Um banco estabelece os preços dos seguros de vida de seus - UNESP 2019
Matemática - 2019Um banco estabelece os preços dos seguros de vida de seus clientes com base no índice de risco do evento assegurado. A tabela mostra o cálculo do índice de risco de cinco eventos diferentes.
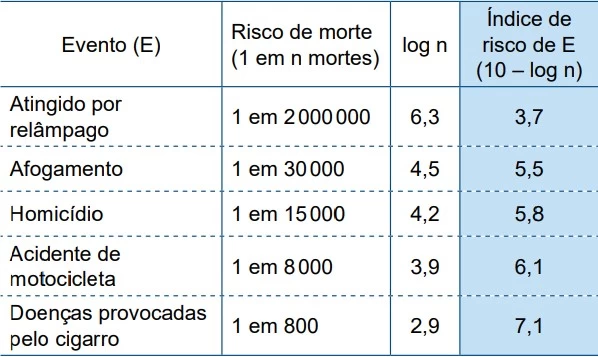
Sabe-se que, nesse banco, o índice de risco de morte pela prática do evento BASE jumping é igual a 8.

Os preços que aparecem no cardápio de um restaurante já - UNICAMP 2019
Matemática - 2019Os preços que aparecem no cardápio de um restaurante já incluem um acréscimo de 10% referente ao total de impostos. Na conta, o valor a ser pago contém o acréscimo de 10% relativo aos serviços (gorjeta).
A nota final de um curso é dada pela média aritmética - UNICAMP 2019
Matemática - 2019A nota final de um curso é dada pela média aritmética simples entre as notas de duas provas e a de um trabalho. Todas as notas se distribuem entre 0 e 10 e a nota final mínima para aprovação é 7.
A representação decimal de certo número inteiro - UNICAMP 2019
Matemática - 2019A representação decimal de certo número inteiro positivo tem dois algarismos. Se o triplo da soma desses algarismos é igual ao próprio número, então o produto dos algarismos é igual a
O sistema de segurança de um aeroporto consiste de duas - UNICAMP 2019
Matemática - 2019O sistema de segurança de um aeroporto consiste de duas inspeções. Na primeira delas, a probabilidade de um passageiro ser inspecionado é de 3/5. Na segunda, a probabilidade se reduz para 1/4.
Sejam a e b números reais positivos. Considere a função - UNICAMP 2019
Matemática - 2019Sejam a e b números reais positivos. Considere a função quadrática f(x) = x(ax + b), definida para todo número real x.
Sejam k e θ números reais tais que sen θ e cos θ são - UNICAMP 2019
Matemática - 2019Sejam k e θ números reais tais que sen θ e cos θ são soluções da equação quadrática 2x2 + x + k = 0. Então, k é um número
No triângulo ABC exibido na figura a seguir, AD é a - UNICAMP 2019
Matemática - 2019No triângulo ABC exibido na figura a seguir, AD é a bissetriz do ângulo interno em A, e 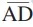 =
= 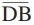 . O ângulo interno em A é igual a
. O ângulo interno em A é igual a
No triângulo ABC exibido na figura a seguir, M é o - UNICAMP 2019
Matemática - 2019No triângulo ABC exibido na figura a seguir, M é o ponto médio do lado AB, e N é o ponto médio do lado AC. Se a área do triângulo MBN é igual a t, então a área do triângulo ABC é igual a
A figura a seguir exibe um pentágono em que quatro lado - UNICAMP 2019
Matemática - 2019A figura a seguir exibe um pentágono em que quatro lados consecutivos têm comprimentos a, b, c e d. Se a sequência (a, b, c, d) é uma progressão geométrica de razão q > 1, então tan θ é igual a
Sabendo que a e b são números reais, considere a matriz - UNICAMP 2019
Matemática - 2019Sabendo que a e b são números reais, considere a matriz quadrada de ordem 3,
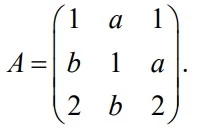
No plano cartesiano, considere a circunferência de - UNICAMP 2019
Matemática - 2019No plano cartesiano, considere a circunferência de equação x2 + y2 − 4y + 3 = 0 e a parábola de equação 3x2 − y + 1 = 0.
Sabendo que a e b são números reais, considere o - UNICAMP 2019
Matemática - 2019Sabendo que a e b são números reais, considere o polinômio cúbico p(x) = x3 + ax2 + x + b. Se a soma e o produto de duas de suas raízes são iguais a −1, então p (1) é igual a
Considere um paralelepípedo retângulo, cujas arestas - UNICAMP 2019
Matemática - 2019Considere um paralelepípedo retângulo, cujas arestas têm comprimento 6 cm, 8 cm e 10 cm, e um triângulo cujos vértices são os centros (intersecção das diagonais) de três faces de dimensões distintas, como ilustra a figura a seguir. O perímetro P desse triângulo é tal que
Uma pesquisa realizada pela Sociedade Brasileira de - FAMERP 2019
Matemática - 2019Uma pesquisa realizada pela Sociedade Brasileira de Cardiologia (SBC) constatou que os níveis elevados de colesterol atingem cerca de quatro em cada dez brasileiros adultos. Isso corresponde a cerca de 60 milhões de pessoas adultas. O estudo ainda revelou que aproximadamente 11% da população adulta brasileira nunca fez exame de colesterol.
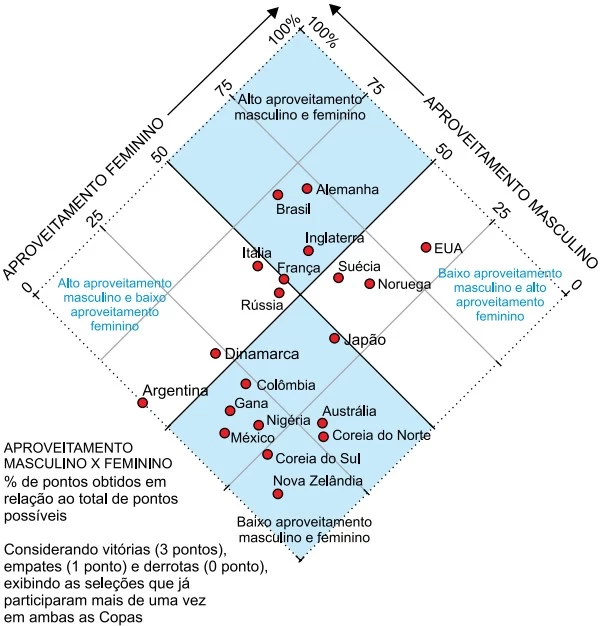
O infográfico indica o desempenho, em termos de - FAMERP 2019
Matemática - 2019O infográfico indica o desempenho, em termos de aproveitamento percentual dos pontos possíveis, das principais seleções de futebol nas categorias masculino e feminino em Copas do Mundo.
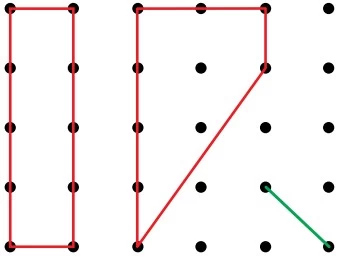
Considere os pontos da malha quadriculada da figura. - FAMERP 2019
Matemática - 2019Considere os pontos da malha quadriculada da figura.
O gráfico de uma função polinomial do 1º grau - FAMERP 2019
Matemática - 2019O gráfico de uma função polinomial do 1º grau f: IR → IR, dada por f(x) = ax + b, é uma reta de coeficiente angular positivo.
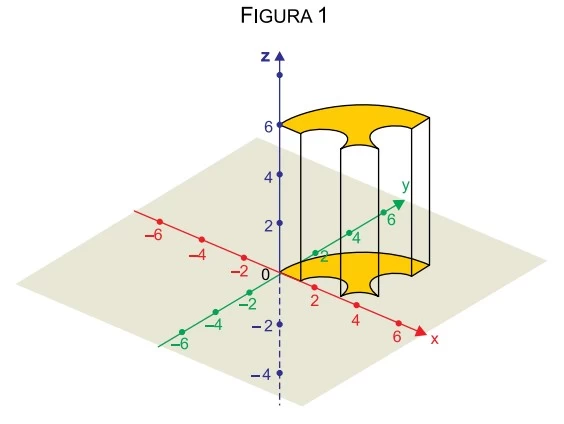
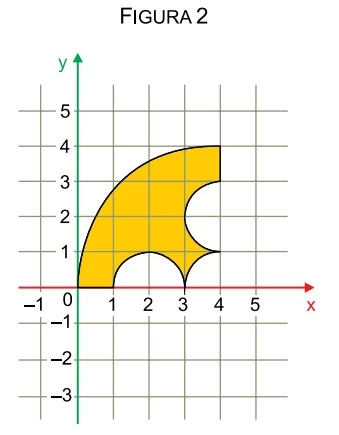
As bases do sólido ilustrado na figura 1, destacadas em - FAMERP 2019
Matemática - 2019As bases do sólido ilustrado na figura 1, destacadas em amarelo, são figuras congruentes contidas em planos paralelos, que distam entre si 6 unidades de comprimento. A base inferior desse sólido, apresentada na figura 2, é limitada por arcos de circunferências centradas em (2, 0), (4, 0) e (4, 2) e por dois segmentos de reta.
Os dados honestos P e Q possuem seis e oito faces - FAMERP 2019
Matemática - 2019Os dados honestos P e Q possuem seis e oito faces, respectivamente. As faces de P estão numeradas com – 2, – 1, 0, 1, 2 e 3. As faces de Q estão numeradas com – 4, – 3, – 2, – 1, 0, 1, 2 e 3.
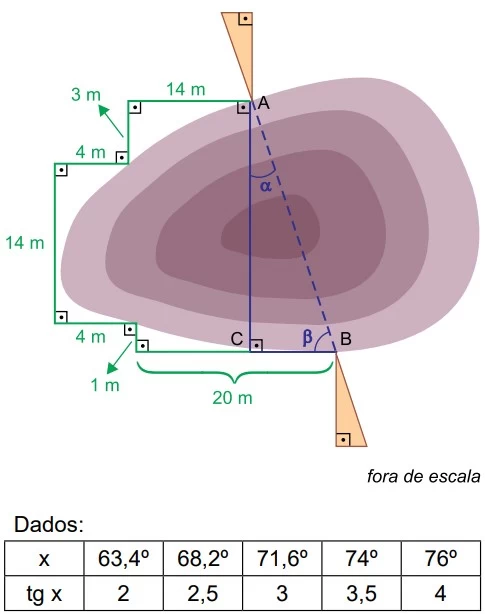
Duas equipes de escavação vão perfurar um túnel — AB em - FAMERP 2019
Matemática - 2019Duas equipes de escavação vão perfurar um túnel  em uma montanha, sendo que uma delas partirá de A e a outra de B, a fim de se encontrarem. Para cavar nas direções corretas os engenheiros precisam determinar as medidas dos ângulos α e β, indicados na figura, que essa direção forma com as retas perpendiculares
em uma montanha, sendo que uma delas partirá de A e a outra de B, a fim de se encontrarem. Para cavar nas direções corretas os engenheiros precisam determinar as medidas dos ângulos α e β, indicados na figura, que essa direção forma com as retas perpendiculares 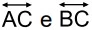 , respectivamente.
, respectivamente.
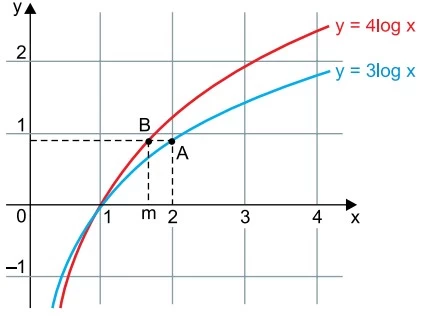
A figura indica os gráficos das funções f e g, definidas - FAMERP 2019
Matemática - 2019A figura indica os gráficos das funções f e g, definidas de 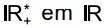 em , cujas leis são, respectivamente, f(x) = 4log x e g(x) = 3log x.
em , cujas leis são, respectivamente, f(x) = 4log x e g(x) = 3log x.
A figura, feita em escala, indica um painel formado por - FAMERP 2019
Matemática - 2019A figura, feita em escala, indica um painel formado por sete retângulos amarelos idênticos e dois retângulos azuis idênticos. Cada retângulo azul tem dimensões x e y, ambas em metros.

A matriz quadrada M = representa uma mensagem codificada - FAMERP 2019
Matemática - 2019A matriz quadrada M = 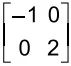 representa uma mensagem codificada. A mensagem decodificada é a matriz quadrada M–1 =
representa uma mensagem codificada. A mensagem decodificada é a matriz quadrada M–1 = 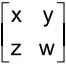 , tal que M–1 é a inversa da matriz M. Sendo assim, o valor de x + y + z + w é
, tal que M–1 é a inversa da matriz M. Sendo assim, o valor de x + y + z + w é
A figura a seguir ilustra, em um sistema de coordenadas cartesianas
Matemática - 2019A figura a seguir ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, um arco e uma flecha retilínea; o arco está tensionado para disparar a flecha.
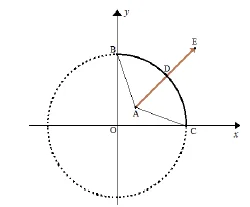
Nesse sistema de coordenadas, uma unidade de medida é o centímetro, e a equação da circunferência, de centro na origem, é expresso por x² + y² = 6,400. O arco tensionado corresponde ao arco da circunferência que está no primeiro quadrante, e as coordenadas do ponto A, ponto de apoio da flecha sobre a corda no momento do disparo, são (20, 20).
Descreva essas informações, julgue o item a seguir.
Se os pontos O, A e D primeiros colineares, e se D para o ponto médio
Matemática - 2019A figura a seguir ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, um arco e uma flecha retilínea; o arco está tensionado para disparar a flecha.

Nesse sistema de coordenadas, uma unidade de medida é o centímetro, e a equação da circunferência, de centro na origem, é expresso por x² + y² = 6,400. O arco tensionado corresponde ao arco da circunferência que está no primeiro quadrante, e as coordenadas do ponto A, ponto de apoio da flecha sobre a corda no momento do disparo, são (20, 20).
Descreva essas informações, julgue o item a seguir.
Se a função f: – {2} → é definida por f(x) = e a - FUVEST 2019
Matemática - 2019
Considere a função polinomial f: → definida por f(x) = - FUVEST 2019
Matemática - 2019Considere a função polinomial f: ℝ → ℝ definida por
f(x) = ax2 + bx + c,
em que a, b, c ∈ ℝ e a ≠ 0. No plano cartesiano xy, a única intersecção da reta y = 2 com o gráfico de f é o ponto (2; 2) e a intersecção da reta x = 0 com o gráfico de f é o ponto (0; –6). O valor de a + b + c é
Um dono de restaurante assim descreveu a evolução do - FUVEST 2019
Matemática - 2019Um dono de restaurante assim descreveu a evolução do faturamento quinzenal de seu negócio, ao longo dos dez primeiros meses após a inauguração: “Até o final dos três primeiros meses, tivemos uma velocidade de crescimento mais ou menos constante, quando então sofremos uma queda abrupta, com o faturamento caindo à metade do que tinha sido atingido. Em seguida, voltamos a crescer, igualando, um mês e meio depois dessa queda, o faturamento obtido ao final do terceiro mês. Agora, ao final do décimo mês, estamos estabilizando o faturamento em um patamar 50% acima do faturamento obtido ao final do terceiro mês”.
Forma-se uma pilha de folhas de papel, em que cada folha - FUVEST 2019
Matemática - 2019Forma-se uma pilha de folhas de papel, em que cada folha tem 0,1 mm de espessura. A pilha é formada da seguinte maneira: coloca-se uma folha na primeira vez e, em cada uma das vezes seguintes, tantas quantas já houverem sido colocadas anteriormente. Depois de 33 dessas operações, a altura da pilha terá a ordem de grandeza
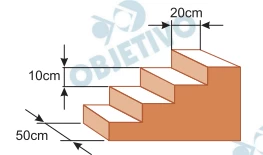
A figura mostra uma escada maciça de quatro degraus, - FUVEST 2019
Matemática - 2019A figura mostra uma escada maciça de quatro degraus, todos eles com formato de um paralelepípedo reto-retângulo. A base de cada degrau é um retângulo de dimensões 20 cm por 50 cm, e a diferença de altura entre o piso e o primeiro degrau e entre os degraus consecutivos é de 10 cm. Se essa escada for prolongada para ter 20 degraus, mantendo o mesmo padrão, seu volume será igual a
Uma empresa estuda cobrir um vão entre dois prédios (com - FUVEST 2019
Matemática - 2019Uma empresa estuda cobrir um vão entre dois prédios (com formato de paralelepípedos reto-retângulos) que têm paredes laterais paralelas, instalando uma lona na forma de um quadrilátero, com pontas presas nos pontos A, B, C e D, conforme indicação da figura.
Sabendo que a lateral de um prédio tem 80 m de altura e 28 m de largura, que a lateral do outro prédio tem 60 m de altura e 20 m de largura e que essas duas paredes laterais distam 15 m uma da outra, a área total dessa lona seria de
Se log2 y = – + log2 x, para x > 0, - FUVEST 2019
Matemática - 2019Se log2 y = – 1/2 + 2/3 log2 x, para x > 0, então
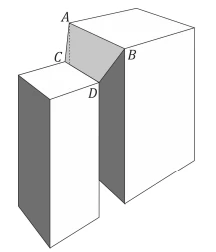
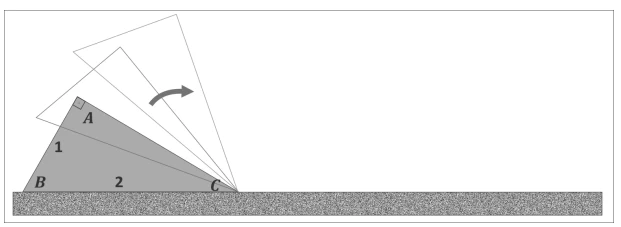
Um triângulo retângulo com vértices denominados A, B e C - FUVEST 2019
Matemática - 2019Um triângulo retângulo com vértices denominados A, B e C apoia-se sobre uma linha horizontal, que corresponde ao solo, e gira sem escorregar no sentido horário. Isto é, se a posição inicial é aquela mostrada na figura, o movimento começa com uma rotação em torno do vértice C até o vértice A tocar o solo, após o que passa a ser uma rotação em torno de A, até o vértice B tocar o solo, e assim por diante.
Uma seta aponta para a posição zero no instante inicial. - FUVEST 2019
Matemática - 2019Uma seta aponta para a posição zero no instante inicial. A cada rodada, ela poderá ficar no mesmo lugar ou mover-se uma unidade para a direita ou mover-se uma unidade para a esquerda, cada uma dessas três possibilidades com igual probabilidade.

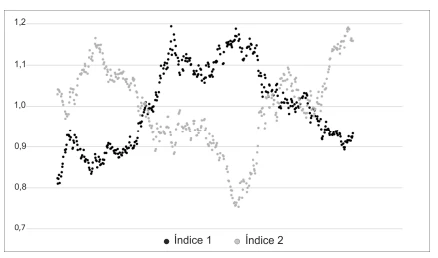
O gráfico mostra a evolução diária, em certo intervalo - FUVEST 2019
Matemática - 2019O gráfico mostra a evolução diária, em certo intervalo de tempo não especificado na abscissa, de dois índices econômicos, normalizados para que suas médias, no mesmo período, sejam ambas iguais a 1. O valor do índice 1 no dia i é xi e o valor do índice 2 no dia i é yi. O gráfico ilustra como cada um dos índices xi e yi varia em função de i, mostrando os pontos (i, xi) (pontos escuros) e (i, yi) (pontos claros).
Um grupo de cinco amigos resolveu passar o final de - FATEC 2019/2
Matemática - 2019Um grupo de cinco amigos resolveu passar o final de semana em um hotel fazenda no interior do estado de São Paulo. Todos foram juntos no mesmo carro e decidiram dividir, igualmente, a despesa total da viagem entre os cinco participantes.

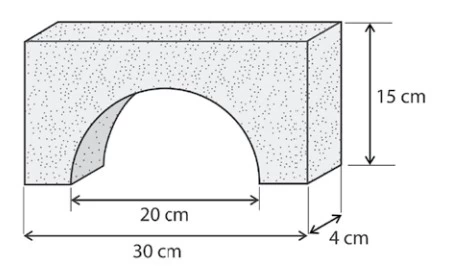
De um paralelepípedo retorretângulo de 30 cm, 4 cm e 15 - FATEC 2019/2
Matemática - 2019De um paralelepípedo retorretângulo de 30 cm, 4 cm e 15 cm, é removido um semicilindro circular reto de altura 4 cm e base de diâmetro 20 cm, obtendo-se uma peça como mostra a figura.

De uma caixa com 50 cartões numerados de 1 a 50, - FATEC 2019/2
Matemática - 2019De uma caixa com 50 cartões numerados de 1 a 50, sorteia-se aleatoriamente um cartão. A probabilidade de que o número sorteado seja divisor de 30 é um valor
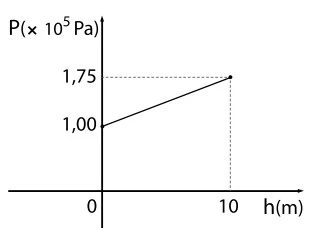
O Teorema de Stevin relaciona a pressão atmosférica e - FATEC 2019/2
Matemática - 2019O Teorema de Stevin relaciona a pressão atmosférica e a pressão nos líquidos. Para um líquido homogêneo, em equilíbrio, cuja superfície está sob ação da pressão atmosférica, a pressão (P) exercida em um ponto submerso qualquer do líquido em relação à altura da coluna de líquido (h) é dada por uma função polinomial do 1.º grau.
O gráfico apresenta a variação da pressão (P) em função da altura da coluna de líquido (h) em um tanque de combustível.
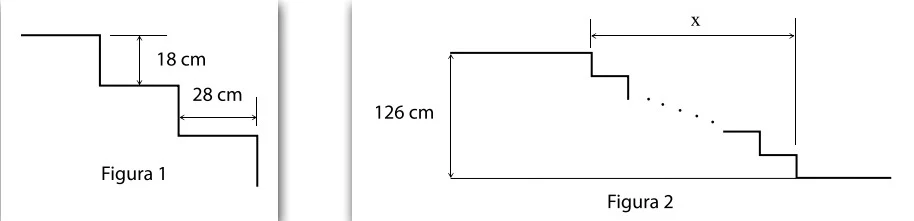
Considere que será construída uma escada para vencer - FATEC 2019/2
Matemática - 2019Considere que será construída uma escada para vencer uma distância vertical de 126 cm. No projeto, todos os degraus têm as mesmas dimensões, conforme a figura 1. A figura 2 apresenta um esquema da escada.
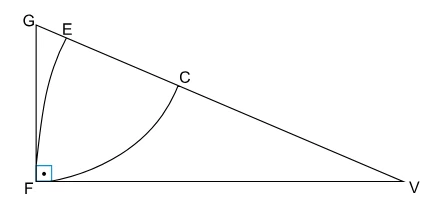
No triângulo retângulo FGV, indicado na figura, FV = 12, FG - FGV 2019
Matemática - 2018No triângulo retângulo FGV, indicado na figura, FV = 12, FG = 5 e os arcos de circunferência FE e CF possuem centros em V e G, respectivamente.
As regras de formação de uma senha de 8 espaços são: 1. O - FGV 2019
Matemática - 2018As regras de formação de uma senha de 8 espaços são:
1. O primeiro espaço tem que ser uma letra do alfabeto.
2. Conter pelo menos um espaço com algarismo.
3. Conter pelo menos um dos caracteres especiais @, #, $, %, &.
4. Qualquer letra do alfabeto pode ser usada em maiúscula ou minúscula.
Nessas condições, o cosseno do ângulo CDN é, - FATEC 2018/2
Matemática - 2018Utilizando um software de desenho 3D, um tecnólogo em Mecânica elaborou o projeto de uma peça de acordo com os seguintes procedimentos:
(1º) no plano cartesiano, desenhou o polígono CDEFGHIJKLMN, conforme figura 1, adotando como unidade de cada eixo coordenado 1 cm.
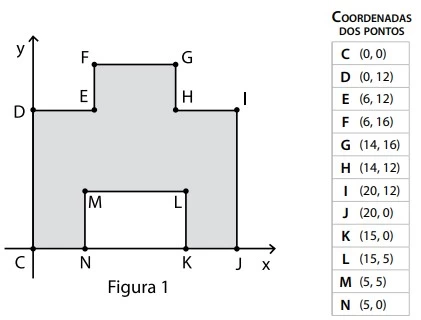
(2º) tendo esse polígono como base, construiu um prisma reto conforme a figura 2.
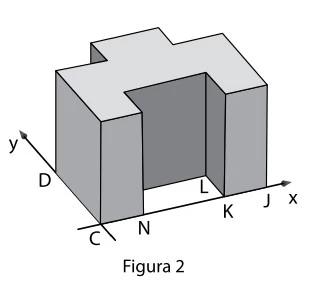
Se a altura do prisma é de 20 cm, então o volume do - FATEC 2018/2
Matemática - 2018Utilizando um software de desenho 3D, um tecnólogo em Mecânica elaborou o projeto de uma peça de acordo com os seguintes procedimentos:
(1º) no plano cartesiano, desenhou o polígono CDEFGHIJKLMN, conforme figura 1, adotando como unidade de cada eixo coordenado 1 cm.

(2º) tendo esse polígono como base, construiu um prisma reto conforme a figura 2.

De acordo com as informações dos gráficos, pode-se - FATEC 2018/2
Matemática - 2018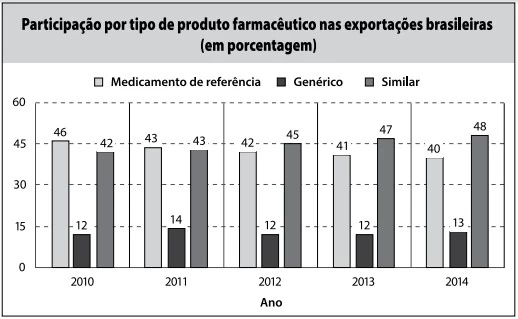
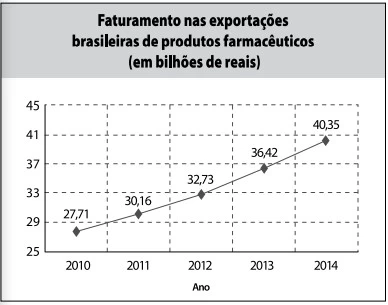
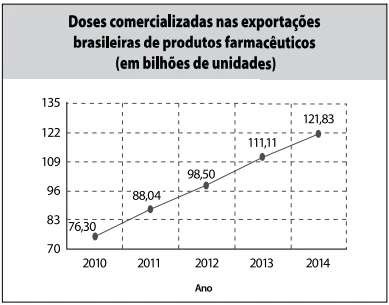
No período de 2010 a 2014, o crescimento no número de - FATEC 2018/2
Matemática - 2018


Considere os dados divulgados pelo Ministério do - FATEC 2018/2
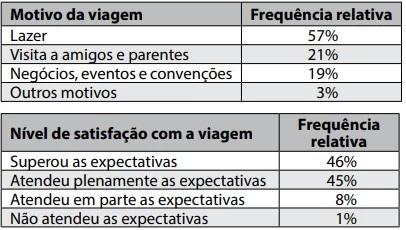
Matemática - 2018Considere os dados divulgados pelo Ministério do Turismo do Brasil em relação à demanda turística internacional em 2016.
Em uma urna, há bolas amarelas, brancas e vermelhas. - FUVEST 2018
Matemática - 2018Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe se que:
I. A probabilidade de retirar uma bola vermelha dessa urna é o dobro da probabilidade de retirar uma bola amarela.
II. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a ser 1/2.
III. Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a ser 1/2.
Sejam f: → e g: + → definidas por f(x) = 5x e g(x) = - FUVEST 2018
Matemática - 2018Sejam f: R → R e g: R+ → definidas por
f(x) = 1/2 5x e g(x) = log10x, respectivamente.
O gráfico da função composta gof é:
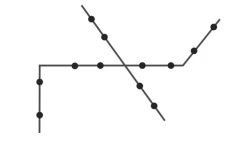
Doze pontos são assinalados sobre quatro segmentos de - FUVEST 2018
Matemática - 2018Doze pontos são assinalados sobre quatro segmentos de reta de forma que três pontos sobre três segmentos distintos nunca são colineares, como na figura.
Dentre os candidatos que fizeram provas de matemática, - FUVEST 2018
Matemática - 2018Dentre os candidatos que fizeram provas de matemática, português e inglês num concurso, 20 obtiveram nota mínima para aprovação nas três disciplinas. Além disso, sabe-se que:
I. 14 não obtiveram nota mínima em matemática;
II. 16 não obtiveram nota mínima em português;
III. 12 não obtiveram nota mínima em inglês;
IV. 5 não obtiveram nota mínima em matemática e em português;
V. 3 não obtiveram nota mínima em matemática e em inglês;
VI. 7 não obtiveram nota mínima em português e em inglês e
VII. 2 não obtiveram nota mínima em português, matemática e inglês.
Sejam Df e Dg os maiores subconjuntos de nos quais - FUVEST 2018
Matemática - 2018Sejam Df e Dg os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais
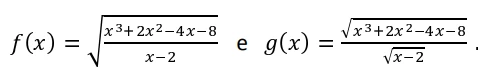
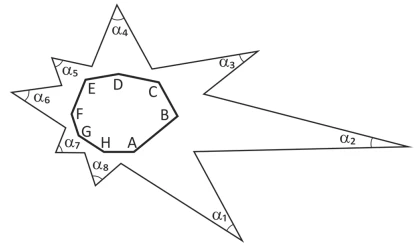
Prolongando-se os lados de um octógono convexo ABCDEFGH, - FUVEST 2018
Matemática - 2018Prolongando-se os lados de um octógono convexo ABCDEFGH, obtém-se um polígono estrelado, conforme a figura.
Admitindo que a linha pontilhada represente o gráfico da - FUVEST 2018
Matemática - 2018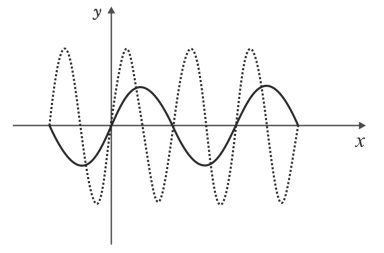
Maria quer comprar uma TV que está sendo vendida por R$ - FUVEST 2018
Matemática - 2018Maria quer comprar uma TV que está sendo vendida por R$ 1.500,00 à vista ou em 3 parcelas mensais sem juros de R$ 500,00. O dinheiro que Maria reservou para essa compra não é suficiente para pagar à vista, mas descobriu que o banco oferece uma aplicação financeira que rende 1% ao mês. Após fazer os cálculos, Maria concluiu que, se pagar a primeira parcela e, no mesmo dia, aplicar a quantia restante, conseguirá pagar as duas parcelas que faltam sem ter que colocar nem tirar um centavo sequer.
Quanto Maria reservou para essa compra, em reais?
Considere o polinômio P(x) = xn + an – 1 xn–1 + … + a1x - FUVEST 2018
Matemática - 2018Considere o polinômio
P(x) = xn + an – 1 xn–1 + … + a1x + a0, em que a0, …, an–1 ∈R .
Sabe-se que as suas n raízes estão sobre a circunferência unitária e que a0 < 0. O produto das n raízes de P(x), para qualquer inteiro n ≥ 1, é:
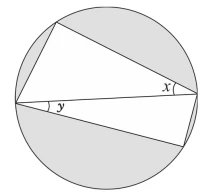
O quadrilátero da figura está inscrito em uma - FUVEST 2018
Matemática - 2018O quadrilátero da figura está inscrito em uma circunferência de raio 1. A diagonal desenhada é um diâmetro dessa circunferência.
Dois atletas correm com velocidades constantes em uma - FUVEST 2018
Matemática - 2018Dois atletas correm com velocidades constantes em uma pista retilínea, partindo simultaneamente de extremos opostos, A e B. Um dos corredores parte de A, chega a B e volta para A. O outro corredor parte de B, chega a A e volta para B. Os corredores cruzam-se duas vezes, a primeira vez a 800 metros de A e a segunda vez a 500 metros de B. O comprimento da pista, em metros, é
Com base no gráfico e nos dados apresentados, escolhido - FATEC 2018
Matemática - 2018Leia o gráfico.
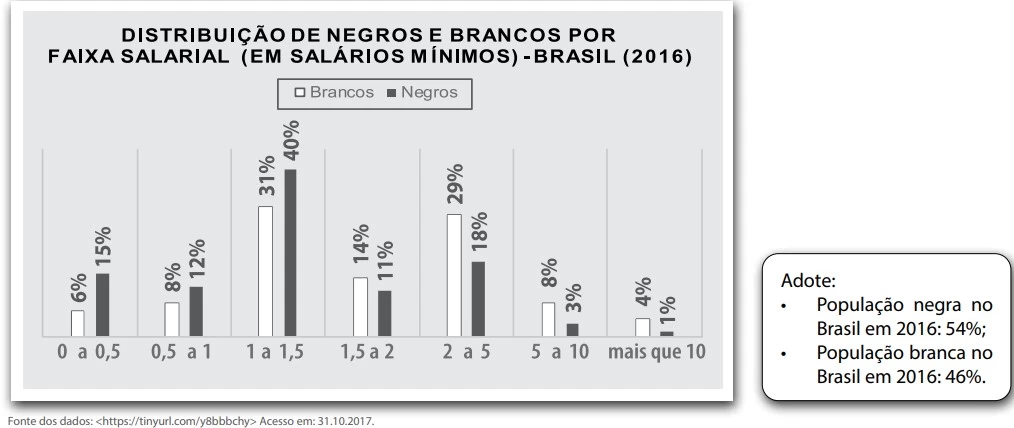
Os salários de um homem branco, uma mulher e um homem - FATEC 2018
Matemática - 2018Os salários de um homem branco, uma mulher e um homem negro foram somados, resultando em R$ 4.380,00.
Sabe-se que o salário dessa mulher é igual a 62% do salário desse homem branco, e o salário desse homem negro é igual a 57% do salário desse homem branco.
No gráfico, o percentual que o volume da pirâmide - FATEC 2018
Matemática - 2018Um artista plástico deseja construir uma obra chamada “A pirâmide da desigualdade da riqueza no Brasil”. Ele fará uma réplica do gráfico apresentado, mantendo todas as suas proporções.

*Nesse gráfico, considere que a altura da pirâmide referente à riqueza dos 10% mais ricos seja 90% da altura da pirâmide total de distribuição de riqueza e que essas pirâmides sejam semelhantes entre si.*
Para construir a obra, ele utilizará quatro triângulos isósceles congruentes entre si e um quadrado, todos feitos de metal, deixando o interior da pirâmide vazio.
A pirâmide terá 4 metros de altura, e a base quadrada terá 6 metros de lado.
Para destacar a diferença entre os mais ricos e os mais - FATEC 2018
Matemática - 2018Um artista plástico deseja construir uma obra chamada “A pirâmide da desigualdade da riqueza no Brasil”. Ele fará uma réplica do gráfico apresentado, mantendo todas as suas proporções.

*Nesse gráfico, considere que a altura da pirâmide referente à riqueza dos 10% mais ricos seja 90% da altura da pirâmide total de distribuição de riqueza e que essas pirâmides sejam semelhantes entre si.*
Para construir a obra, ele utilizará quatro triângulos isósceles congruentes entre si e um quadrado, todos feitos de metal, deixando o interior da pirâmide vazio.
A pirâmide terá 4 metros de altura, e a base quadrada terá 6 metros de lado.
O total de metal necessário para construir essa obra será - FATEC 2018
Matemática - 2018Um artista plástico deseja construir uma obra chamada “A pirâmide da desigualdade da riqueza no Brasil”. Ele fará uma réplica do gráfico apresentado, mantendo todas as suas proporções.

*Nesse gráfico, considere que a altura da pirâmide referente à riqueza dos 10% mais ricos seja 90% da altura da pirâmide total de distribuição de riqueza e que essas pirâmides sejam semelhantes entre si.*
Para construir a obra, ele utilizará quatro triângulos isósceles congruentes entre si e um quadrado, todos feitos de metal, deixando o interior da pirâmide vazio.
A pirâmide terá 4 metros de altura, e a base quadrada terá 6 metros de lado.
Dentre os cinco bancos com maior número de agências - INSPER 2018
Matemática - 2018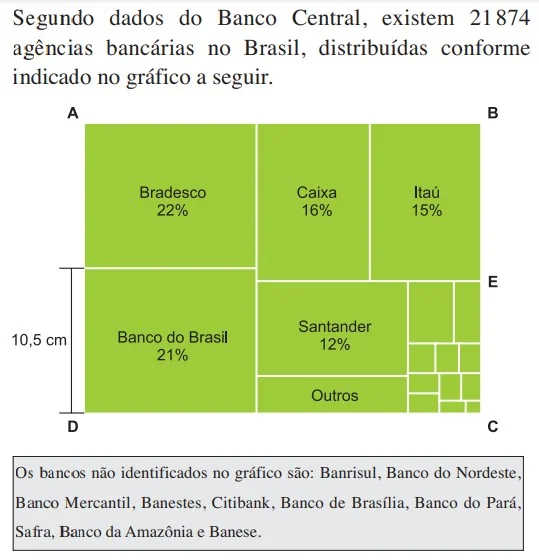
Considerando que o retângulo ABCD está - INSPER 2018
Matemática - 2018
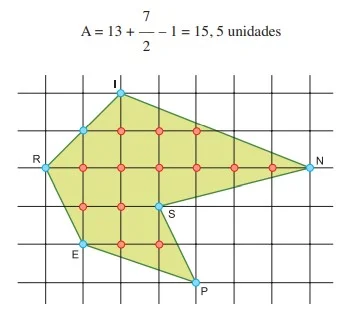
De acordo com o teorema de Pick, se os vértices de um - INSPER 2018
Matemática - 2018De acordo com o teorema de Pick, se os vértices de um polígono simples estão sobre uma grade de pontos de coordenadas inteiras, sua área será igual a i + P/2 - 1, sendo i o número de pontos de coordenadas inteiras no interior do polígono e p o número de pontos de coordenadas inteiras no perímetro do polígono. Por exemplo, a área A do polígono INSPER, indicado na figura, é
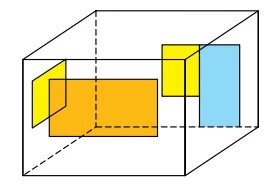
Uma sala possui três janelas e uma porta, como indica - UNESP 2018/2
Matemática - 2018Uma sala possui três janelas e uma porta, como indica a figura.
Apoie nosso trabalho!
Assine Agora