Matemática
Exibindo questões de 501 a 600.
O coeficiente de x12 na expansão de (1 + x4 + x5) 10 é - FGV 2017
Matemática - 2017O coeficiente de x12 na expansão de (1 + x4 + x5)10
Somando todos os números de três algarismos distintos que - FGV 2017
Matemática - 2017Somando todos os números de três algarismos distintos que podem ser formados com os dígitos 1, 2, 3 e 4,
Para todos os inteiros n de 1 a 2016, temos que: - FGV 2017
Matemática - 2017Para todos os inteiros n de 1 a 2016, temos que:
Uma parábola P1 de equação y = x2 + bx + c, quando - FGV 2017
Matemática - 2017Uma parábola P1 de equação y = x2 + bx + c, quando refletida em relação ao eixo x, gera a parábola P2. Transladando horizontalmente P1 e P2 em sentidos opostos, por quatro unidades, obtemos parábolas de equações y = f(x) e y = g(x).
Certo capital foi aplicado em regime de juros compostos. - FGV 2017
Matemática - 2017Certo capital foi aplicado em regime de juros compostos. Nos quatro primeiros meses, a taxa foi de 1% ao mês e, nos quatro meses seguintes, a taxa foi de 2% ao mês. Sabendo-se que, após os oito meses de aplicação, o montante resgatado foi de R$ 65.536,00, então o capital aplicado, em reais, foi aproximadamente igual a
O dono de uma papelaria comprou uma grande quantidade de - FGV 2017
Matemática - 2017O dono de uma papelaria comprou uma grande quantidade de canetas de dois tipos, A e B, ao preço de R$ 20,00 e R$ 15,00 a dúzia, respectivamente, tendo pago na compra o valor de R$ 1.020,00. No total, ele saiu da loja com 777 canetas, mas sabe-se que, para cada três dúzias de um mesmo tipo de caneta que comprou, ele ganhou uma caneta extra, do mesmo tipo, de brinde.
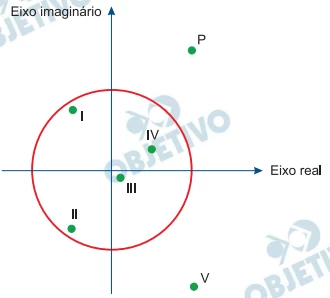
Seja Z um número complexo cujo afixo P está localizado no - FGV 2017
Matemática - 2017Seja Z um número complexo cujo afixo P está localizado no 1o. quadrante do plano complexo, e sejam I, II, III, IV e V os afixos de cinco outros números complexos, conforme indica a figura seguinte.
Na representação gráfica do sistema de equações - FGV 2017
Matemática - 2017Na representação gráfica do sistema de equações
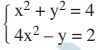
A única solução da equação sen 2x . sen 3x = cos 2x . cos 3 - FGV 2017
Matemática - 2017A única solução da equação
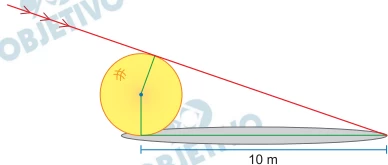
Uma esfera de raio r está apoiada sobre o chão plano em um - FGV 2017
Matemática - 2017Uma esfera de raio r está apoiada sobre o chão plano em um dia iluminado pelo sol. Em determinado horário, a sombra projetada à direita do ponto onde a esfera toca o chão tinha comprimento de 10 m, como indica a figura.
Probabilidade de ocorrência do evento A é igual a - FGV 2017
Matemática - 2017A probabilidade de ocorrência do evento A é igual a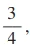 e a de ocorrência do evento B é igual a
e a de ocorrência do evento B é igual a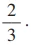
O volume do cilindro circular reto que se obtém aumentando - FGV 2017
Matemática - 2017O volume do cilindro circular reto que se obtém aumentando-se x metros no raio da base desse cilindro, com x ≠ 0, é igual ao do que se obtém aumentando-se x metros na sua altura.
O total de números de cinco algarismos que possuem pelo - FGV 2017
Matemática - 2017O total de números de cinco algarismos que possuem pelo menos dois dígitos consecutivos iguais
A média aritmética das notas de cinco provas de estatística - FGV 2018
Matemática - 2017A média aritmética das notas de cinco provas de estatística é 6,4. Retirando-se a prova com a menor nota, a nova média aritmética sobe para 7,0. Agora, retirando-se a prova com a maior nota, a nova média aritmética das três provas remanescentes abaixa para 6,5.
Uma lista de quatro números inteiros tem média 7 e - FGV 2018
Matemática - 2017Uma lista de quatro números inteiros tem média 7 e diferença entre o maior e o menor dos números igual a 24. A moda e a mediana da lista são, ambas, iguais a 8.
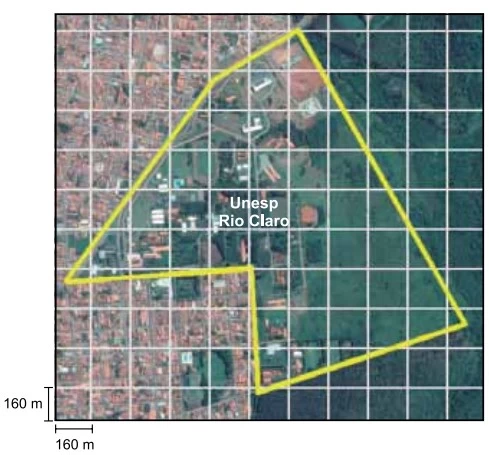
O hexágono marcado na malha quadriculada sobre a - UNESP 2017
Matemática - 2017O hexágono marcado na malha quadriculada sobre a fotografia representa o contorno do câmpus da Unesp de Rio Claro, que é aproximadamente plano.
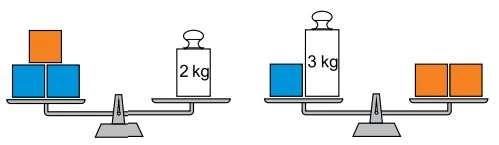
Três cubos laranjas idênticos e três cubos azuis - UNESP 2017
Matemática - 2017Três cubos laranjas idênticos e três cubos azuis idênticos estão equilibrados em duas balanças de pratos, também idênticas, conforme indicam as figuras.
Uma companhia de engenharia de trânsito divulga o índice - UNESP 2017
Matemática - 2017Uma companhia de engenharia de trânsito divulga o índice de lentidão das ruas por ela monitoradas de duas formas distintas, porém equivalentes. Em uma delas, divulga-se a quantidade de quilômetros congestionados e, na outra, a porcentagem de quilômetros congestionados em relação ao total de quilômetros monitorados.
A figura indica o empilhamento de três cadeiras idênticas - UNESP 2017
Matemática - 2017A figura indica o empilhamento de três cadeiras idênticas e perfeitamente encaixadas umas nas outras, sendo h a altura da pilha em relação ao chão.

No universo dos números reais, a equação é satisfeita por - UNESP 2017
Matemática - 2017No universo dos números reais, a equação
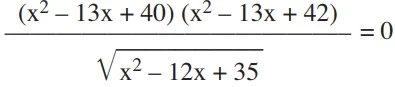
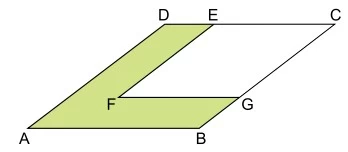
Na figura, o losango FGCE possui dois lados sobrepostos - UNESP 2017
Matemática - 2017Na figura, o losango FGCE possui dois lados sobrepostos aos do losango ABCD e sua área é igual à área indicada em verde.
Em um jogo de tabuleiro, o jogador desloca seu peão nas - UNESP 2017
Matemática - 2017Em um jogo de tabuleiro, o jogador desloca seu peão nas casas por meio dos pontos obtidos no lançamento de um par de dados convencionais e não viciados. Se o jogador obtém números diferentes nos dados, ele avança um total de casas igual à soma dos pontos obtidos nos dados, encerrando-se a jogada. Por outro lado. se o jogador obtém números iguais nos dados, ele lança novamente o par de dados e avança seu peão pela soma dos pontos obtidos nos dois lançamentos, encerrando-se a jogada.
A figura a seguir indica a posição do peão no tabuleiro desse jogo antes do início de uma jogada.

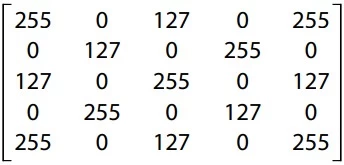
Uma matriz M = (aij), quadrada de ordem 5, em que i - FATEC 2017
Matemática - 2017Uma tela de computador pode ser representada por uma matriz de cores, de forma que cada elemento da matriz corresponda a um pixel* na tela.
Numa tela em escala de cinza, por exemplo, podemos atribuir 256 cores diferentes para cada pixel, do preto absoluto (código da cor: 0) passando pelo cinza intermediário (código da cor: 127) ao branco absoluto (código da cor: 255).
*Menor elemento em uma tela ao qual é possível atribuir-se uma cor.
Suponha que na figura estejam representados 25 pixels de uma tela.

A matriz numérica correspondente às cores da figura apresentada é dada por
O número máximo de matrizes distintas que podem ser - FATEC 2017
Matemática - 2017Uma tela de computador pode ser representada por uma matriz de cores, de forma que cada elemento da matriz corresponda a um pixel* na tela.
Numa tela em escala de cinza, por exemplo, podemos atribuir 256 cores diferentes para cada pixel, do preto absoluto (código da cor: 0) passando pelo cinza intermediário (código da cor: 127) ao branco absoluto (código da cor: 255).
*Menor elemento em uma tela ao qual é possível atribuir-se uma cor.
Suponha que na figura estejam representados 25 pixels de uma tela.

A matriz numérica correspondente às cores da figura apresentada é dada por

Suponha a existência de uma espécie C1 de cigarras, - FATEC 2017
Matemática - 2017Os Estados Unidos se preparam para uma invasão de insetos após 17 anos
Elas vivem a pelo menos 20 centímetros sob o solo há 17 anos. E neste segundo trimestre, bilhões de cigarras (Magicicada septendecim) emergirão para invadir partes da Costa Leste, enchendo os céus e as árvores, e fazendo muito barulho.
Há mais de 170 espécies de cigarras na América do Norte, e mais de 2 mil espécies ao redor do mundo. A maioria aparece todos os anos, mas alguns tipos surgem a cada 13 ou 17 anos. Os visitantes deste ano, conhecidos como Brood II (Ninhada II, em tradução livre) foram vistos pela última vez em 1996. Os moradores da Carolina do Norte e de Connecticut talvez tenham de usar rastelos e pás para retirá-las do caminho, já que as estimativas do número de insetos são de 30 bilhões a 1 trilhão.
Um estudo brasileiro descobriu que intervalos baseados em números primos ofereciam a melhor estratégia de sobrevivência para as cigarras.
O texto afirma que os habitantes das áreas próximas às - FATEC 2017
Matemática - 2017Os Estados Unidos se preparam para uma invasão de insetos após 17 anos
Elas vivem a pelo menos 20 centímetros sob o solo há 17 anos. E neste segundo trimestre, bilhões de cigarras (Magicicada septendecim) emergirão para invadir partes da Costa Leste, enchendo os céus e as árvores, e fazendo muito barulho.
Há mais de 170 espécies de cigarras na América do Norte, e mais de 2 mil espécies ao redor do mundo. A maioria aparece todos os anos, mas alguns tipos surgem a cada 13 ou 17 anos. Os visitantes deste ano, conhecidos como Brood II (Ninhada II, em tradução livre) foram vistos pela última vez em 1996. Os moradores da Carolina do Norte e de Connecticut talvez tenham de usar rastelos e pás para retirá-las do caminho, já que as estimativas do número de insetos são de 30 bilhões a 1 trilhão.
Um estudo brasileiro descobriu que intervalos baseados em números primos ofereciam a melhor estratégia de sobrevivência para as cigarras.
Com relação à Ninhada II, e adotando o ano de 1996 como o - FATEC 2017
Matemática - 2017Os Estados Unidos se preparam para uma invasão de insetos após 17 anos
Elas vivem a pelo menos 20 centímetros sob o solo há 17 anos. E neste segundo trimestre, bilhões de cigarras (Magicicada septendecim) emergirão para invadir partes da Costa Leste, enchendo os céus e as árvores, e fazendo muito barulho.
Há mais de 170 espécies de cigarras na América do Norte, e mais de 2 mil espécies ao redor do mundo. A maioria aparece todos os anos, mas alguns tipos surgem a cada 13 ou 17 anos. Os visitantes deste ano, conhecidos como Brood II (Ninhada II, em tradução livre) foram vistos pela última vez em 1996. Os moradores da Carolina do Norte e de Connecticut talvez tenham de usar rastelos e pás para retirá-las do caminho, já que as estimativas do número de insetos são de 30 bilhões a 1 trilhão.
Um estudo brasileiro descobriu que intervalos baseados em números primos ofereciam a melhor estratégia de sobrevivência para as cigarras.
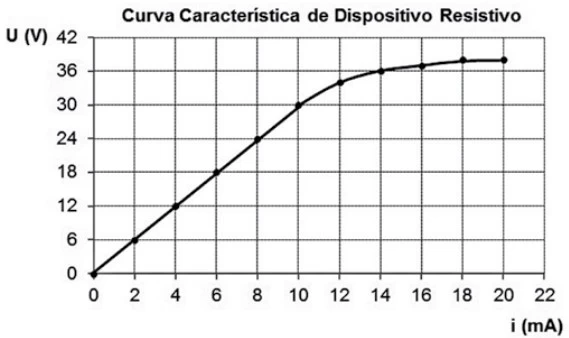
Em uma disciplina de circuitos elétricos da FATEC, o - FATEC 2017
Matemática - 2017Em uma disciplina de circuitos elétricos da FATEC, o Professor de Física pede aos alunos que determinem o valor da resistência elétrica de um dispositivo com comportamento inicial ôhmico, ou seja, que obedece à primeira Lei de Ohm. Para isso, os alunos utilizam um multímetro ideal de precisão e submetem o dispositivo a uma variação na diferença de potencial elétrico anotando os respectivos valores das correntes elétricas observadas. Dessa forma, eles decidem construir um gráfico contendo a curva característica do dispositivo resistivo, apresentada na figura.
Sabe-se que, em um grupo de 10 pessoas, o livro A foi - UNICAMP 2017
Matemática - 2017Sabe-se que, em um grupo de 10 pessoas, o livro A foi lido por 5 pessoas e o livro B foi lido por 4 pessoas.
Um dado não tendencioso de seis faces será lançado duas - UNICAMP 2017
Matemática - 2017Um dado não tendencioso de seis faces será lançado duas vezes. A probabilidade de que o maior valor obtido nos lançamentos seja menor do que 3 é igual a
Seja 𝑓(𝑥) uma função tal que para todo número real - UNICAMP 2017
Matemática - 2017Seja ?(?) uma função tal que para todo número real ? temos que ??(? − 1) = (? − 3)?(?) + 3. Então, ?(1) é igual a
Durante o vestibular da FATEC, um candidato levou - FATEC 2017/2
Matemática - 2017Leia o texto e o ínfográfico, relacionados a dados referentes ao ano de 2015, para responder às questões de números 30 a 32.

O relatório anual “Tendências Globais”, que registra o deslocamento forçado ao redor do mundo, aponta um total de 65,3 milhões de pessoas deslocadas por guerras e conflitos até o final de 2015 – um aumento de quase 10% se comparado com o total de 59,5 milhões registrado em 2014. Esta é a primeira vez que o deslocamento forçado ultrapassa o marco de 60 milhões de pessoas.
No final de 2005, o Alto Comissariado das Nações Unidas para Refugiados (ACNUR) registrou uma média de 6 pessoas deslocadas a cada minuto. Hoje (2015), esse número é de 24 por minuto.
O universo de 65,3 milhões inclui 21,3 milhões de refugiados ao redor do mundo, 3,2 milhões de solicitantes de refúgio e 40,8 milhões de deslocados que continuam dentro de seus países.
Considere as funções f(x) = 3x e g(x) = x3, definidas - UNICAMP 2017
Matemática - 2017Considere as funções f(x) = 3x e g(x) = x3, definidas para todo número real x. O número de soluções da equação f(g(x)) = g(f(x)) é igual a
Com os dados apresentados, podemos afirmar corretamente - FATEC 2017/2
Matemática - 2017Leia o texto e o ínfográfico, relacionados a dados referentes ao ano de 2015, para responder às questões de números 30 a 32.

O relatório anual “Tendências Globais”, que registra o deslocamento forçado ao redor do mundo, aponta um total de 65,3 milhões de pessoas deslocadas por guerras e conflitos até o final de 2015 – um aumento de quase 10% se comparado com o total de 59,5 milhões registrado em 2014. Esta é a primeira vez que o deslocamento forçado ultrapassa o marco de 60 milhões de pessoas.
No final de 2005, o Alto Comissariado das Nações Unidas para Refugiados (ACNUR) registrou uma média de 6 pessoas deslocadas a cada minuto. Hoje (2015), esse número é de 24 por minuto.
O universo de 65,3 milhões inclui 21,3 milhões de refugiados ao redor do mundo, 3,2 milhões de solicitantes de refúgio e 40,8 milhões de deslocados que continuam dentro de seus países.
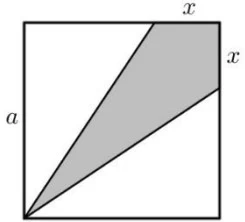
Considere o quadrado de lado a > 0 exibido na figura - UNICAMP 2017
Matemática - 2017Considere o quadrado de lado a > 0 exibido na figura abaixo. Seja A(x) a função que associa a cada 0 ≤ x ≤ a a área da região indicada pela cor cinza.
Suponha um aumento exato de 10% no número de pessoas de - FATEC 2017/2
Matemática - 2017Leia o texto e o ínfográfico, relacionados a dados referentes ao ano de 2015, para responder às questões de números 30 a 32.

O relatório anual “Tendências Globais”, que registra o deslocamento forçado ao redor do mundo, aponta um total de 65,3 milhões de pessoas deslocadas por guerras e conflitos até o final de 2015 – um aumento de quase 10% se comparado com o total de 59,5 milhões registrado em 2014. Esta é a primeira vez que o deslocamento forçado ultrapassa o marco de 60 milhões de pessoas.
No final de 2005, o Alto Comissariado das Nações Unidas para Refugiados (ACNUR) registrou uma média de 6 pessoas deslocadas a cada minuto. Hoje (2015), esse número é de 24 por minuto.
O universo de 65,3 milhões inclui 21,3 milhões de refugiados ao redor do mundo, 3,2 milhões de solicitantes de refúgio e 40,8 milhões de deslocados que continuam dentro de seus países.
Considere a circunferência de equação cartesiana x2 + - UNICAMP 2017
Matemática - 2017Considere a circunferência de equação cartesiana x2 + y2 = x − y.
Admita que a população da Síria em 2010 era de 20,7 - FATEC 2017/2
Matemática - 2017Admita que a população da Síria em 2010 era de 20,7 milhões de habitantes e em 2016, principalmente pelo grande número de mortes e da imigração causados pela guerra civil, o número de habitantes diminuiu para 17,7 milhões.
Considere que durante esse período, o número de habitantes da Síria, em milhões, possa ser descrito por uma função h, polinomial do 1º grau, em função do tempo (x), em número de anos.
Sendo a um número real, considere a matriz A = . Então - UNICAMP 2017
Matemática - 2017Sendo a um número real, considere a matriz 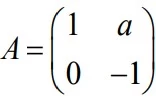 .
.
A maior parte dos refugiados sírios que solicita abrigo - FATEC 2017/2
Matemática - 2017A maior parte dos refugiados sírios que solicita abrigo na Europa escolhe a Alemanha como destino. No entanto, muitos refugiados sírios têm vindo também para o Brasil. Considere o triângulo ABC no qual o vértice A representa a cidade de Aleppo, na Síria; o vértice B representa a cidade de Berlim, na Alemanha, e o vértice C representa a cidade de Campinas, no Brasil.
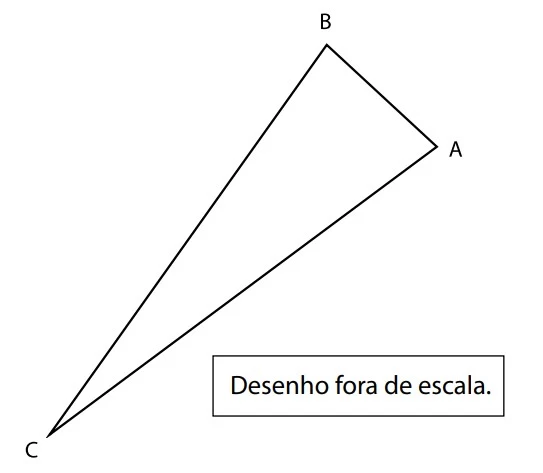
Nesse triângulo, a distância entre A e B é de 3 700 km, a medida de  é igual a 18° e a medida de
é igual a 18° e a medida de 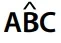 é igual a 81°.
é igual a 81°.
Com base nos dados apresentados, se um refugiado sírio viaja de Aleppo a Berlim e, em seguida, de Berlim a Campinas, terá percorrido no mínimo x quilômetros em todo o trajeto.
Sejam a e b números reais. Considere, então, os dois - UNICAMP 2017
Matemática - 2017Sejam a e b números reais. Considere, então, os dois sistemas lineares abaixo, nas variáveis x, y e z:
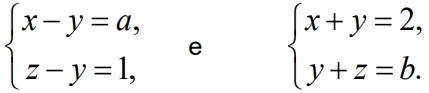
Considere o polinômio p(x) = xn + xm + 1, em que n > m - UNICAMP 2017
Matemática - 2017Considere o polinômio p(x) = xn + xm + 1, em que n > m ≥ 1. Se o resto da divisão de p(x) por x + 1 é igual a 3, então
Seja i a unidade imaginária, isto é, i2 = −1. O lugar - UNICAMP 2017
Matemática - 2017Seja i a unidade imaginária, isto é, i2 = −1. O lugar geométrico dos pontos do plano cartesiano com coordenadas reais (x, y) tais que (2x + yi)(y + 2xi) = i é uma
Um paralelepípedo retângulo tem faces de áreas 2 cm2, - UNICAMP 2017
Matemática - 2017Um paralelepípedo retângulo tem faces de áreas 2 cm2, 3 cm2 e 4 cm2.
Seja x um número real, 0 < x < π/2, tal que a sequência - UNICAMP 2017
Matemática - 2017Seja x um número real, 0 < x < π/2, tal que a sequência (tan x, sec x, 2) é uma progressão aritmética (PA).
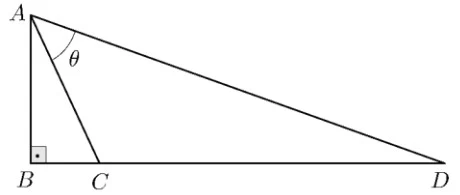
Considere o triângulo retângulo ABD exibido na figura - UNICAMP 2017
Matemática - 2017Considere o triângulo retângulo ABD exibido na figura abaixo, em que AB = 2 cm, BC = 1 cm e CD = 5 cm.
Em certa espécie animal a proporção de nucleotídeos - UNICAMP 2017
Matemática - 2017Em certa espécie animal a proporção de nucleotídeos Timina na molécula de DNA é igual a t > 0. Então, a proporção de nucleotídeos Citosina nesse mesmo DNA é igual a
Na língua portuguesa, a ordem dos algarismos de acordo - UNICAMP 2017
Matemática - 2017Observe a tirinha abaixo.

Um copo inicialmente vazio foi enchido com água por meio - FAMERP 2017
Matemática - 2017Um copo inicialmente vazio foi enchido com água por meio de uma torneira com vazão constante. O gráfico mostra a altura da água no copo em função do tempo durante seu enchimento até a boca.

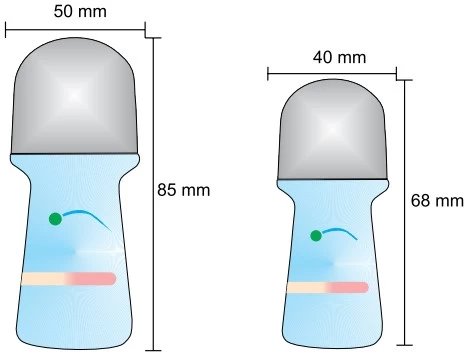
Um desodorante é vendido em duas embalagens de tamanhos - FAMERP 2017
Matemática - 2017Um desodorante é vendido em duas embalagens de tamanhos diferentes, porém de formatos matematicamente semelhantes. A figura indica algumas das medidas dessas embalagens.
De acordo com a Organização Mundial da Saúde, a - FAMERP 2017
Matemática - 2017De acordo com a Organização Mundial da Saúde, a população adulta deveria consumir, no máximo, até 2 gramas de sódio por dia, o que equivale, para cada indivíduo adulto, a uma colher de chá rasa de sal de cozinha refinado por dia.
A escala de coma de Glasgow é utilizada como primeira - FAMERP 2017
Matemática - 2017A escala de coma de Glasgow é utilizada como primeira avaliação do nível de consciência de pacientes com trauma craniano. Essa escala consiste em avaliar o paciente em três testes, que são: ocular (O), verbal (V) e motor (M). O especialista que avalia o paciente atribui de 1 a 4 pontos para O, de 1 a 5 pontos para V e de 1 a 6 pontos para M. Um trauma cranioencefálico é considerado grave se a pontuação total é de 3 a 8 pontos, moderado se é de 9 a 13 pontos, e leve se é de 14 a 15 pontos.
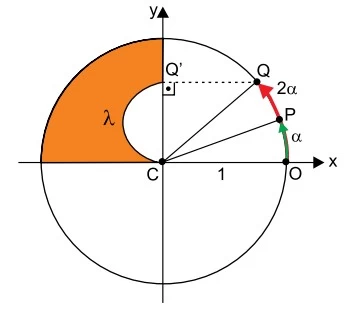
Em uma circunferência trigonométrica de centro C e - FAMERP 2017
Matemática - 2017Em uma circunferência trigonométrica de centro C e origem dos arcos em O, foram marcados os pontos P e Q, sendo que as medidas dos arcos  são iguais, respectivamente, a α e 2α, conforme indica a figura.
são iguais, respectivamente, a α e 2α, conforme indica a figura.
O banco de sangue de um hospital possui 100 bolsas de - FAMERP 2017
Matemática - 2017O banco de sangue de um hospital possui 100 bolsas de sangue, cada uma obtida de um doador diferente. As bolsas estão distribuídas por grupo sanguíneo, conforme mostra a tabela.
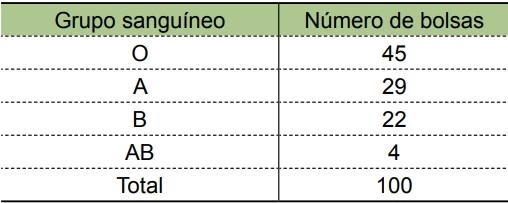
A figura mostra os gráficos de duas funções polinomiais - FAMERP 2017
Matemática - 2017A figura mostra os gráficos de duas funções polinomiais do 1º grau, f e g, num mesmo sistema cartesiano ortogonal, sendo que o gráfico de f passa pela origem.
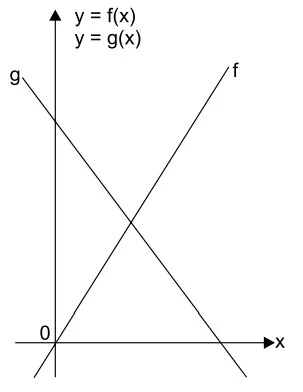
A figura mostra, em perspectiva, as quatro primeiras - FAMERP 2017
Matemática - 2017A figura mostra, em perspectiva, as quatro primeiras pilhas de blocos de uma sequência.
No estudo da dinâmica de populações é comum ser - FAMERP 2017
Matemática - 2017No estudo da dinâmica de populações é comum ser necessário determinar o número real λ na equação det (M – λI) = 0, em que M é uma matriz quadrada, I é a matriz identidade, da mesma ordem de M, e det representa o determinante da matriz (M – λI).
Em 1996, 25% da energia produzida por um país era obtida - FAMERP 2017
Matemática - 2017Em 1996, 25% da energia produzida por um país era obtida de usinas hidrelétricas. Em 2016, essa produção passou a ser de 40%.
O Ministério da Saúde e os estados brasileiros - UNESP 2016/2
Matemática - 2016O Ministério da Saúde e os estados brasileiros investigaram 3 670 casos suspeitos de microcefalia em todo o país. O boletim de 02 de fevereiro aponta que, desse total, 404 tiveram confirmação de microcefalia ou de outras alterações do sistema central, e outros 709 casos foram descartados. Anteriormente, no boletim de 23 de janeiro, havia 732 casos investigados e classificados como confirmados ou como descartados.
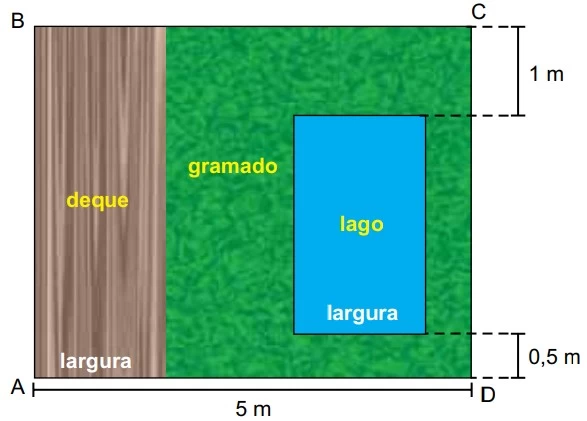
Em um terreno retangular ABCD, de 20 m2, serão - UNESP 2016/2
Matemática - 2016Em um terreno retangular ABCD, de 20 m2, serão construídos um deque e um lago, ambos de superfícies retangulares de mesma largura, com as medidas indicadas na figura. O projeto de construção ainda prevê o plantio de grama na área restante, que corresponde a 48% do terreno.
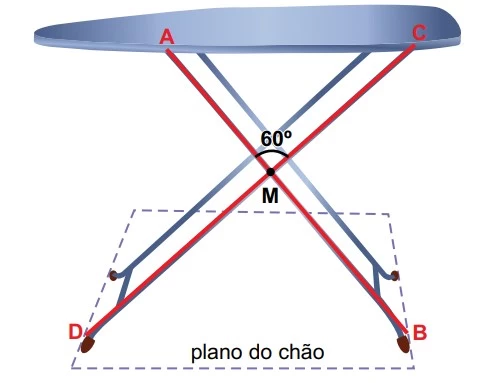
Um mesa de passar roupa possui pernas articuladas - UNESP 2016/2
Matemática - 2016Um mesa de passar roupa possui pernas articuladas ??̅̅̅̅ e ??̅̅̅̅, conforme a figura. Sabe-se que AB=CD=1m, e que M é ponto médio dos segmentos coplanares ??̅̅̅̅ e ??̅̅̅̅. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo ??̂? é 60º.
Em um experimento com sete palitos de fósforo idênticos - UNESP 2016/2
Matemática - 2016Em um experimento com sete palitos de fósforo idênticos, seis foram acesos nas mesmas condições e ao mesmo tempo. A chama de cada palito foi apagada depois de t segundos e, em seguida, anotou-se o comprimento x, em centímetros, de madeira não chamuscada em cada palito. A figura a seguir indica os resultados do experimento.

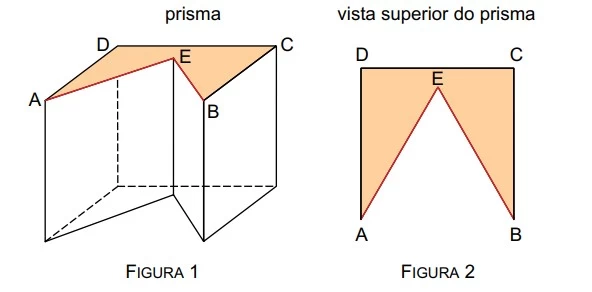
Um cubo com aresta de medida igual a x centímetros foi - UNESP 2016/2
Matemática - 2016Um cubo com aresta de medida igual a x centímetros foi seccionado, dando origem ao prisma indicado na figura 1. A figura 2 indica a vista superior desse prisma, sendo que AEB é um triângulo equilátero.
Uma colher foi solta 978 vezes ao acaso em direção ao - UNESP 2016/2
Matemática - 2016Uma colher foi solta 978 vezes ao acaso em direção ao chão. O registro da posição em que ela caiu sobre o chão está indicado na tabela.

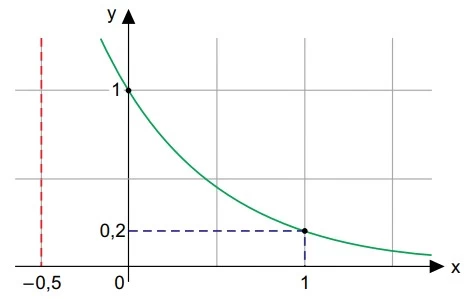
A figura descreve o gráfico de uma função exponencial - UNESP 2016/2
Matemática - 2016A figura descreve o gráfico de uma função exponencial do tipo y = ax, de R em R.
Um ponto P, de coordenadas (x, y) do plano cartesiano - UNESP 2016/2
Matemática - 2016Sendo assim, o resultado da multiplicação matricial 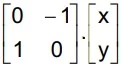 é uma matriz coluna que, no plano cartesiano ortogonal, necessariamente representa um ponto que é
é uma matriz coluna que, no plano cartesiano ortogonal, necessariamente representa um ponto que é
Uma loja reajustou em 20% o preço de certo modelo de - FGV 2016
Matemática - 2016Uma loja reajustou em 20% o preço de certo modelo de televisão. Todavia, diante da queda nas vendas, a loja pretende dar um desconto sobre o preço reajustado de modo a voltar ao preço inicial.
Uma empresa fabrica x unidades de uma peça de automóvel - FGV 2016
Matemática - 2016Uma empresa fabrica x unidades de uma peça de automóvel a um custo total mensal dado por C(x) = 10000 + a.x, em que 10 000 é o custo fixo e a é o custo variável por unidade.
Em janeiro foram fabricadas e vendidas 1 000 peças a um custo médio de R$ 60,00.
Se, em fevereiro, o preço de venda de cada peça for R$ 75,00, qual a quantidade mínima a ser fabricada e vendida para a empresa não ter prejuízo?
Um capital aplicado a juros compostos a uma certa taxa - FGV 2016
Matemática - 2016Um capital aplicado a juros compostos a uma certa taxa anual de juros dobra a cada 7 anos.
Assinale a sentença verdadeira: a) Dois lados de um - FGV 2016
Matemática - 2016Assinale a sentença
No plano cartesiano, a reta de equação 3x + 4y = 17 - FGV 2016
Matemática - 2016No plano cartesiano, a reta de equação 3x + 4y = 17 tangencia uma circunferência de centro no ponto (1,1).
No plano cartesiano, os pontos (x,y) que satisfazem a - FGV 2016
Matemática - 2016No plano cartesiano, os pontos (x,y) que satisfazem a equação x2 – 5x + 4 = 0
O gráfico abaixo exibe o lucro líquido (em milhares de - UNICAMP 2016
Matemática - 2016O gráfico abaixo exibe o lucro líquido (em milhares de reais) de três pequenas empresas A, B e C, nos anos de 2013 e 2014.

Em 2013, uma empresa exportou 600 mil dólares e, em 2014, e - FGV 2016
Matemática - 2016Em 2013, uma empresa exportou 600 mil dólares e, em 2014, exportou 650 mil dólares de um certo produto. Suponha que o gráfico das exportações y (em milhares de dólares) em função do ano x seja formado por pontos colineares.
Uma moeda balanceada é lançada quatro vezes, - UNICAMP 2016
Matemática - 2016Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a
Um automóvel 0 km é vendido por certo valor em 15/6/2016. - FGV 2016
Matemática - 2016Um automóvel 0 km é vendido por certo valor em 15/6/2016.
No dia 15/6 de cada ano, seu valor será 10% menor do que era no mesmo dia do ano anterior, isto é, desvaloriza-se 10% ao ano.
Em uma matriz, chamam-se elementos internos aqueles que - UNICAMP 2016
Matemática - 2016Em uma matriz, chamam-se elementos internos aqueles que não pertencem à primeira nem à última linha ou coluna.
Uma progressão aritmética (PA) é constituída de 15 números - FGV 2016
Matemática - 2016Uma progressão aritmética (PA) é constituída de 15 números inteiros com razão igual a 2.
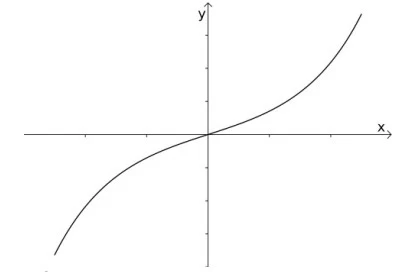
Considere o gráfico da função y = f(x) exibido na - UNICAMP 2016
Matemática - 2016Considere o gráfico da função y = f(x) exibido na figura a seguir
Dada a matriz B = e sabendo que a matriz A–1 = é a matriz - FGV 2016
Matemática - 2016Dada a matriz B = 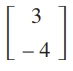 e sabendo que a matriz
e sabendo que a matriz 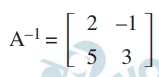 é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a equação matricial AX = B,
é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a equação matricial AX = B,
Considere a função afim f(x) = ax + b definida para - UNICAMP 2016
Matemática - 2016Considere a função afim f(x) = ax + b definida para todo número real x, onde a e b são números reais.
Um cinema cobra R$ 30,00 por ingresso. Estudantes e idosos - FGV 2016
Matemática - 2016Um cinema cobra R$ 30,00 por ingresso. Estudantes e idosos pagam meia entrada, isto é, R$ 15,00 por ingresso. Para uma sessão, foram vendidos 300 ingressos e a receita correspondente foi R$ 7 200,00.
A solução da equação na variável real x, logx(x + 6) - UNICAMP 2016
Matemática - 2016A solução da equação na variável real x, logx(x + 6) = 2, é um número
Em uma urna, há 4 bolas vermelhas e 5 bolas brancas. - FGV 2016
Matemática - 2016Em uma urna, há 4 bolas vermelhas e 5 bolas brancas. Sorteando-se sucessivamente 3 bolas sem reposição,
Seja (a, b, c) uma progressão geométrica de números - UNICAMP 2016
Matemática - 2016Seja (a, b, c) uma progressão geométrica de números reais com a ≠ 0. Definindo s = a + b + c, o menor valor possível para s/a é igual a
O número de quartos ocupados em um hotel varia de acordo - FGV 2016
Matemática - 2016O número de quartos ocupados em um hotel varia de acordo com a época do ano. Estima-se que o número de quartos ocupados em cada mês de determinado ano seja dado por Q(x) = 150 + 30 cos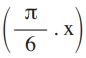 em que x é estabelecido da seguinte forma: x = 1 representa o mês de janeiro, x = 2 representa o mês de fevereiro, x = 3 representa o mês de março, e assim por diante.
em que x é estabelecido da seguinte forma: x = 1 representa o mês de janeiro, x = 2 representa o mês de fevereiro, x = 3 representa o mês de março, e assim por diante.
Considere o sistema linear nas variáveis reais x, y, z - UNICAMP 2016
Matemática - 2016Considere o sistema linear nas variáveis reais x, y, z e w.
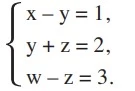
14 Um dos fatores do polinômio P(x) = x3 + 2x2 – 5x – 6 é - FGV 2016
Matemática - 2016Um dos fatores do polinômio P(x) = x3 + 2x2 – 5x – 6 é (x + 3).
Considere a matriz quadrada de ordem 3, A = , onde x é - UNICAMP 2016
Matemática - 2016Considere a matriz quadrada de ordem 3,  , onde x é um número real.
, onde x é um número real.
Um investidor brasileiro analisa duas opções de aplicação - FGV 2016
Matemática - 2016Um investidor brasileiro analisa duas opções de aplicação de seu capital em reais por um ano:
1a. opção: Aplicar o capital em reais no Brasil ganhando 15% ao ano.
2a. opção: Converter seu capital de reais para dólares, aplicar o valor obtido nos EUA por um ano à taxa de 2% ao ano e, em seguida, trocar os dólares por reais.
Considerando os dados abaixo:
• 1 dólar na data de aplicação vale A reais,
• 1 dólar na data do recebimento do montante vale B reais,
Considere o círculo de equação cartesiana x2 + y2 = ax - UNICAMP 2016
Matemática - 2016Considere o círculo de equação cartesiana x2 + y2 = ax + by, onde a e b são números reais não nulos.
A figura abaixo exibe um quadrilátero ABCD, onde AB = - UNICAMP 2016
Matemática - 2016A figura abaixo exibe um quadrilátero ABCD, onde AB = AD e BC = CD = 2 cm. A área do quadrilátero ABCD é igual a
Um cilindro circular reto, cuja altura é igual ao - UNICAMP 2016
Matemática - 2016Um cilindro circular reto, cuja altura é igual ao diâmetro da base, está inscrito numa esfera.
Considere o polinômio cúbico p(x) = x3 + x2 – ax – 3 - UNICAMP 2016
Matemática - 2016Considere o polinômio cúbico p(x) = x3 + x2 – ax – 3, onde a é um número real.
Considere o número complexo z = , onde a é um número - UNICAMP 2016
Matemática - 2016Considere o número complexo z = 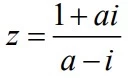 , onde a é um número real e i é a unidade imaginária, isto é, i2 = – 1. O valor de z2016 é igual a
, onde a é um número real e i é a unidade imaginária, isto é, i2 = – 1. O valor de z2016 é igual a
Pode-se afirmar, em relação à distribuição do número de - FATEC 2016
Matemática - 2016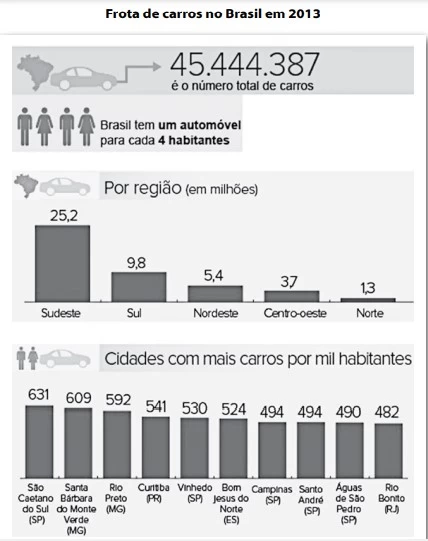
Admita que, em 2013, Águas de São Pedro (SP) possuía - FATEC 2016
Matemática - 2016
Com base nas informações do infográfico, podemos afirmar - FATEC 2016
Matemática - 2016
Um atossegundo é uma unidade de tempo que representa um - FATEC 2016
Matemática - 2016Um atossegundo é uma unidade de tempo que representa um bilionésimo de um bilionésimo de segundo. Um femtossegundo é também uma unidade de tempo que representa um milionésimo de um bilionésimo de segundo. Sabe-se que o processo que permite a visão depende da interação da luz com pigmentos da retina e leva cerca de 200 femtossegundos para ocorrer
Em 2015, um arranha-céu de 204 metros de altura foi - FATEC 2016
Matemática - 2016Em 2015, um arranha-céu de 204 metros de altura foi construído na China em somente 19 dias, utilizando um modelo de arquitetura modular pré-fabricada. Suponha que o total de metros de altura construídos desse prédio varie diariamente, de acordo com uma Progressão Aritmética (PA), de primeiro termo igual a 12,5 metros (altura construída durante o primeiro dia), e o último termo da PA igual a x metros (altura construída durante o último dia).
Apoie nosso trabalho!
Assine Agora