Matemática
Exibindo questões de 401 a 500.
Os menores lados de uma folha de papel retangular de - UNESP 2018/2
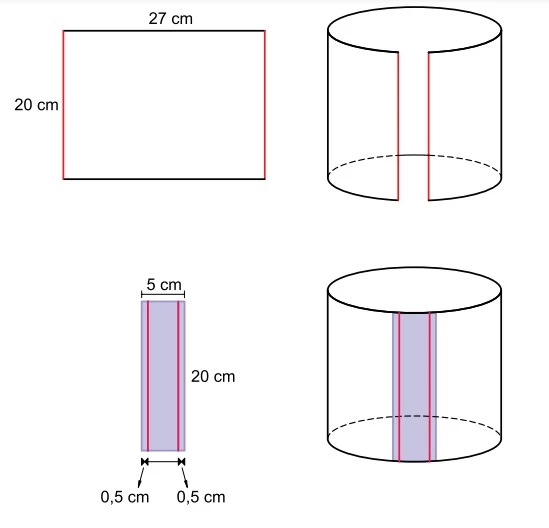
Matemática - 2018Os menores lados de uma folha de papel retangular de 20 cm por 27 cm foram unidos com uma fita adesiva retangular de 20 cm por 5 cm, formando um cilindro circular reto vazado.
Na união, as partes da fita adesiva em contato com a folha correspondem a dois retângulos de 20 cm por 0,5 cm, conforme indica a figura.
O gráfico indica o número de vítimas fatais no trânsito - UNESP 2018/2
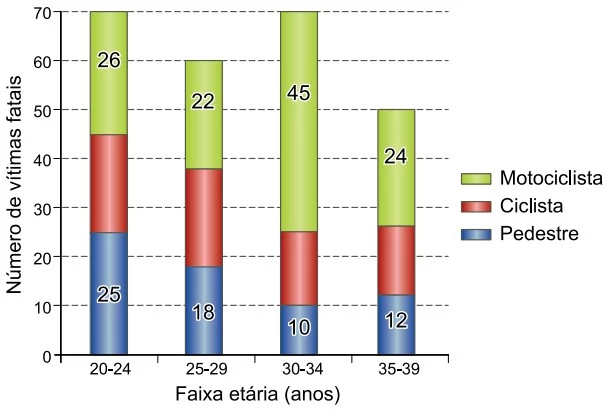
Matemática - 2018O gráfico indica o número de vítimas fatais no trânsito de uma grande cidade em 2017. Os dados estão distribuídos por quatro faixas etárias e por três categorias de locomoção dessas vítimas: pedestres, ciclistas e motociclistas.
Sendo x um número real maior que , a área de um - UNESP 2018/2
Matemática - 2018Sendo x um número real maior que 2/3, a área de um retângulo é dada pelo polinômio 3x2 + 19x –14.
Dois dados convencionais e honestos foram lançados ao - UNESP 2018/2
Matemática - 2018Dois dados convencionais e honestos foram lançados ao acaso. Sabendo-se que saiu o número 6 em pelo menos um deles, a probabilidade de que tenha saído o número 1 no outro é igual a
A figura mostra cinco retângulos justapostos de uma - UNESP 2018/2
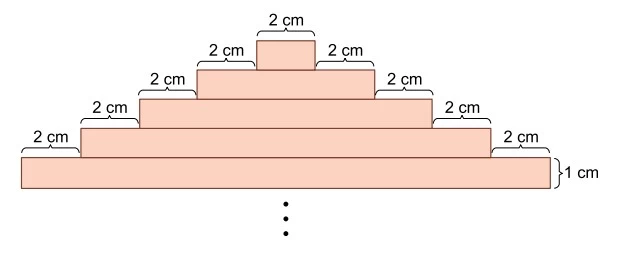
Matemática - 2018A figura mostra cinco retângulos justapostos de uma sequência. Todos os retângulos possuem mesma altura, igual a 1 cm.
Observe, no plano cartesiano de eixos ortogonais, - UNESP 2018/2
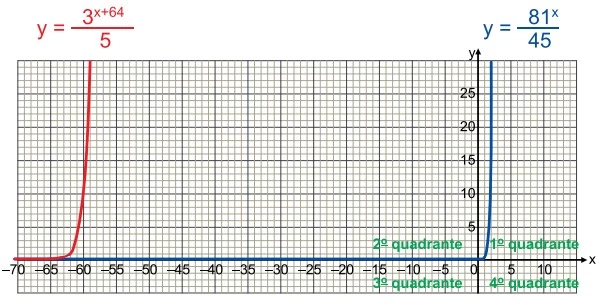
Matemática - 2018Observe, no plano cartesiano de eixos ortogonais, o gráfico de duas funções exponenciais de R em R.
Observe a figura da representação dos pontos M e N - UNESP 2018/2
Matemática - 2018Observe a figura da representação dos pontos M e N sobre a superfície da Terra.
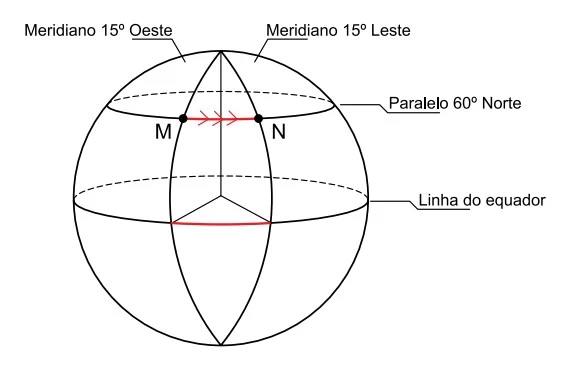
Sendo m e n números reais, a operação m☆n é definida como s - FGV 2018
Matemática - 2018Sendo m e n números reais, a operação m☆n é definida como sendo igual a 2-m-n. Observe dois exemplos de uso dessa simbologia:

Rita compra bijuterias para revender. Em julho, ela - FGV 2018
Matemática - 2018Rita compra bijuterias para revender. Em julho, ela comprou 3 pulseiras iguais e 10 colares iguais, pagando, no total, R$ 87,00. Em agosto, ela comprou 10 das mesmas pulseiras, com desconto de 10%, e 25 dos mesmos colares, com acréscimo de 10%, gastando, nessa compra, R$ 243,00.
A equação quadrática x2 – 2x + c = 0, em que c é uma const - FGV 2018
Matemática - 2018A equação quadrática x2 – 2x + c = 0, em que c é uma constante real, tem como raízes x1 e x2
O polinômio P(x) = 6x2 – 5x + k2, em que k é uma constante - FGV 2018
Matemática - 2018O polinômio P(x) = 6x2 – 5x + k, em que k é uma constante real, tem 3x – 4 como um de seus fatores.
Observe o gráfico de uma função g, definida pela lei y = g - FGV 2018
Matemática - 2018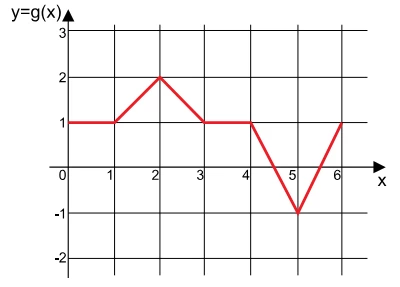
O valor do número real b para o qual a igualdade - FGV 2018
Matemática - 2018O valor do número real b para o qual a igualdade
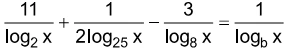
Dados, em um plano α, uma reta d e um ponto F fora dela, a - FGV 2018
Matemática - 2018Dados, em um plano α, uma reta d e um ponto F fora dela, a parábola é o lugar geométrico dos pontos de α equidistantes de d e de F.
Os termos de uma sequência são definidos recursivamente - FGV 2018
Matemática - 2018Os termos de uma sequência são definidos recursivamente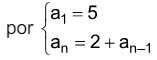
Uma aplicação financeira de C reais à taxa mensal de juros - FGV 2018
Matemática - 2018Uma aplicação financeira de C reais à taxa mensal de juros compostos de x% é resgatada depois de 8 meses no montante igual a C8 reais. Sendo assim,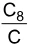
A figura representa uma semicircunferência de diâmetro CD - FGV 2018
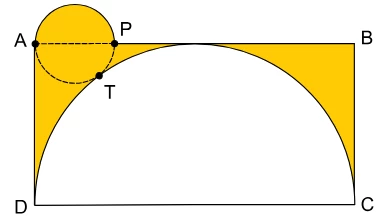
Matemática - 2018A figura representa uma semicircunferência de diâmetro CD, perfeitamente inscrita no retângulo ABCD. Sabe-se que P é um ponto de AB, e que AP é diâmetro da circunferência que tangencia a semicircunferência maior em T.
A figura indica três cartas, A, B e C, cada uma com um - FGV 2018
Matemática - 2018A figura indica três cartas, A, B e C, cada uma com um número inteiro positivo no verso.

Um telhado retangular ABCD tem área igual a 120 m2 e está - FGV 2018
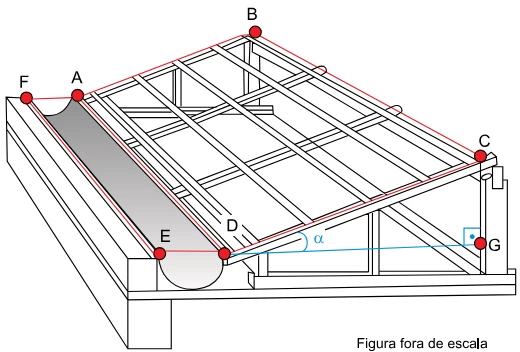
Matemática - 2018Um telhado retangular ABCD tem área igual a 120 m2 e está conectado a uma calha de escoamento de água da chuva. A calha tem a forma de um semicilindro reto, de diâmetro AF = DE = 0,4 m e capacidade igual a 720 litros.
O produto do quadrado das potências de dois que vão, em - FGV 2018
Matemática - 2018O produto do quadrado das potências de dois que vão, em sequência aritmética, de 2 até x é igual a y, o que se traduz por meio da igualdade 22 . 42 . 82 · 162 . 322. ... . x2 = y, com x e y sendo números naturais.
Seja A = (aij) 22 uma matriz tal que aij - FGV 2018
Matemática - 2018Seja A = (aij)22 uma matriz tal que aij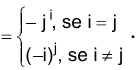
Em um curso de graduação da UFT, um quinto dos acadêmicos tem altura
Matemática - 2018Em um curso de graduação da UFT, um quinto dos acadêmicos tem altura menor que 1,60 metros, metade tem altura de 1,60 a 1,70 metros e 75 acadêmicos têm mais de 1,70 metros.
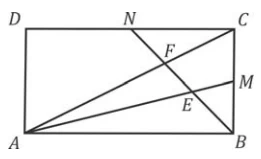
Seja ABCD um paralelogramo e AP , BQ, CR e - FGV 2018
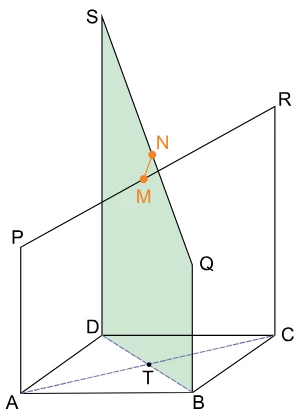
Matemática - 2018Seja ABCD um paralelogramo e AP , BQ, CR e DS segmen tos contidos em retas paralelas entre si, localizados do mesmo lado do plano que contém o paralelogramo ABCD. Sabe-se que AP = 10, BQ = 8, CR = 18, DS = 22, T é ponto de intersecção entre AC e BD, e que M e N são, respectivamente, pontos médios de PR e QS, como mostra a figura.
Sabe-se da trigonometria que sen2 θ + cos2 θ = 1. Um - FGV 2018
Matemática - 2018Sabe-se da trigonometria que sen2 θ + cos2 θ = 1. Um triângulo ABC possui coordenadas A(–6, 0), B(6, 0), C(6 cosθ, 6 senθ), com θ ∈ IR e sen θ ≠ 0.
Sejam m e n números reais e um sistema de equações nas - FGV 2018
Matemática - 2018Sejam m e n números reais e 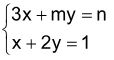
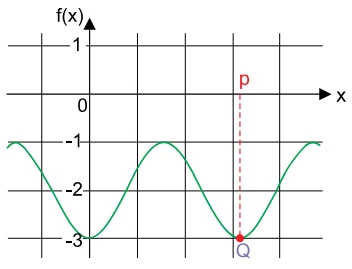
Observe o gráfico de uma função trigonométrica cosseno, - FGV 2018
Matemática - 2018Observe o gráfico de uma função trigonométrica cosseno, dada pela expressão f(x) = m + ncos(2x), sendo m, n e p números reais, com ponto de mínimo em x = p, que é a abscissa do ponto Q.
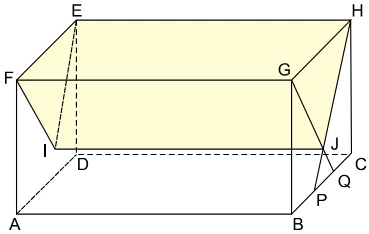
Sobre a face quadrada BCHG do paralelepípedo retoretângulo - FGV 2018
Matemática - 2018Sobre a face quadrada BCHG do paralelepípedo retoretângulo ABCDEFGH foram traçados GQ e HP, intersectando-se em J, com P e Q dividindo BC em três segmentos congruentes tais que BP = PQ = QC. Sabe-se ainda que HE = 8 cm e que GJHEFI é um prisma reto de volume 81 cm³..
Um triângulo isósceles ABC, com AB = AC = 1, é tal que - FGV 2018
Matemática - 2018Um triângulo isósceles ABC, com AB = AC = 1, é tal que cada ângulo da base BC mede o dobro do ângulo de vértice A.
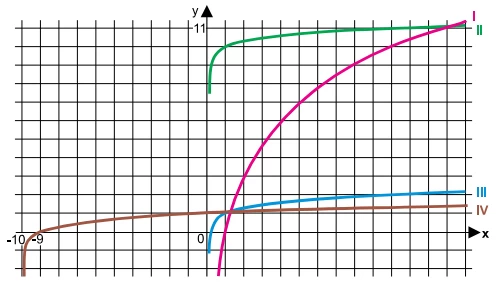
As funções logarítmicas f, g, h, p são dadas por f(x) = 10 - FGV 2018
Matemática - 2018As funções logarítmicas f, g, h, p são dadas por f(x) = 10 + log x, g(x) = 10log x, h(x) = log(10x) e p(x) = log(x + 10). Observe os gráficos a seguir:
Uma caixa contém 100 bolas de mesmo formato, peso e - FGV 2018
Matemática - 2018Uma caixa contém 100 bolas de mesmo formato, peso e textura, sendo algumas brancas e outras pretas. Sorteando-se ao acaso, e com reposição, uma bola duas vezes, a pro babilidade de que em ambos os sorteios saia uma bola preta é igual a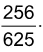
Considere três números inteiros cuja soma é um número - UNICAMP 2018
Matemática - 2018Considere três números inteiros cuja soma é um número ímpar. Entre esses três números, a quantidade de números ímpares é igual a
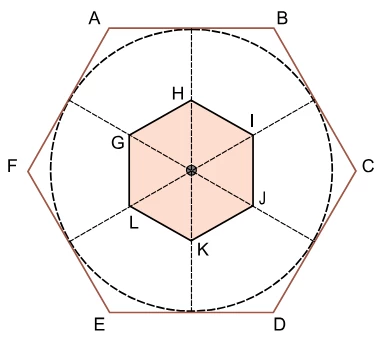
A figura indica um hexágono regular ABCDEF, de área S1 , e - FGV 2018
Matemática - 2018A figura indica um hexágono regular ABCDEF, de área S1, e um hexágono regular GHIJKL, de vértices nos pontos médios dos apótemas do hexágono ABCDEF e área S2.
Dois anos atrás certo carro valia R$ 50.000,00 e - UNICAMP 2018
Matemática - 2018Dois anos atrás certo carro valia R$ 50.000,00 e atualmente vale R$ 32.000,00. Supondo que o valor do carro decresça a uma taxa anual constante, daqui a um ano o valor do carro será igual a
Existe quantidade ilimitada de bolas de três cores - FGV 2018
Matemática - 2018Existe quantidade ilimitada de bolas de três cores diferentes (branca, preta, azul) em um depósito, sendo que as bolas se diferenciam apenas pela cor. Oito dessas bolas serão colocadas em uma caixa.
Lançando-se determinada moeda tendenciosa, a - UNICAMP 2018
Matemática - 2018Lançando-se determinada moeda tendenciosa, a probabilidade de sair cara é o dobro da probabilidade de sair coroa.
Considere o sistema de inequações dado por: A região do - FGV 2018
Matemática - 2018Considere o sistema de inequações dado por:
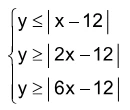
Seja a função h(x) definida para todo número real x por - UNICAMP 2018
Matemática - 2018Seja a função h(x) definida para todo número real x por
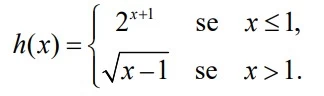
A solução gráfica do sistema de inequações - FGV 2018
Matemática - 2018A solução gráfica do sistema de inequações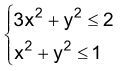
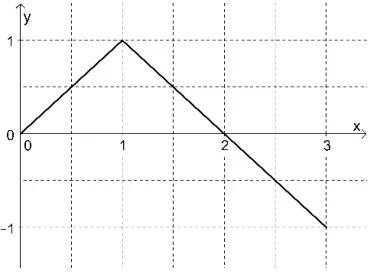
A figura a seguir exibe o gráfico de uma função y = - UNICAMP 2018
Matemática - 2018A figura a seguir exibe o gráfico de uma função y = f(x) para 0 ≤ x ≤ 3.
Um trapézio é delimitado pelos eixos x e y do plano - FGV 2018
Matemática - 2018Um trapézio é delimitado pelos eixos x e y do plano cartesiano e pelas retas de equações y = 2x + 1 e x = 4.
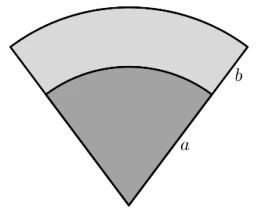
A figura abaixo exibe um setor circular dividido em - UNICAMP 2018
Matemática - 2018A figura abaixo exibe um setor circular dividido em duas regiões de mesma área. A razão a/b é igual a
Duas pessoas combinaram de se encontrar entre 12h00 e 13h00 - FGV 2018
Matemática - 2018Duas pessoas combinaram de se encontrar entre 12h00 e 13h00. Elas também combinaram de esperar até 20 minutos pela outra pessoa depois de chegar ao local do encontro. Assumindo que os horários de chegada ao local de encontro são uniformemente distribuídos no intervalo de uma hora, que vai das 12h00 às 13h00,
Considere que o quadrado ABCD, representado na figura - UNICAMP 2018
Matemática - 2018Considere que o quadrado ABCD, representado na figura abaixo, tem lados de comprimento de 1 cm, e que C é o ponto médio do segmento AE. Consequentemente, a distância entre os pontos D e E será igual a
Seja x um número real tal que sen x + cos x = 0,2. Logo - UNICAMP 2018
Matemática - 2018Seja x um número real tal que sen x + cos x = 0,2. Logo, |sen x − cos x| é igual a
Sejam a e b números reais tais que a matriz A = - UNICAMP 2018
Matemática - 2018Sejam a e b números reais tais que a matriz A = 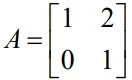 satisfaz a equação A2 = aA + bI, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
satisfaz a equação A2 = aA + bI, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
Sabendo que k é um número real, considere o sistema - UNICAMP 2018
Matemática - 2018Sabendo que k é um número real, considere o sistema linear nas variáveis reais x e y,
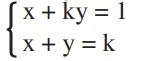
No plano cartesiano, sejam C a circunferência de centro - UNICAMP 2018
Matemática - 2018No plano cartesiano, sejam C a circunferência de centro na origem e raio r > 0 e s a reta de equação x + 3y = 10.
Sejam p(x) e q(x) polinômios com coeficientes reais. - UNICAMP 2018
Matemática - 2018Sejam p(x) e q(x) polinômios com coeficientes reais. Dividindo-se p(x) por q(x), obtêm-se quociente e resto iguais a x2 + 1.
Sejam a e b números reais não nulos. Se o número - UNICAMP 2018
Matemática - 2018Sejam a e b números reais não nulos. Se o número complexo z = a + bi é uma raiz da equação quadrática x2 + bx + a = 0, então
Em 2016, um determinado país teve T casos de cânceres em - FAMERP 2018
Matemática - 2018Em 2016, um determinado país teve T casos de cânceres em homens, dos quais 64% correspondiam aos dez tipos mais frequentes. Sabe-se que 30% dos dez tipos mais frequentes correspondiam ao câncer de próstata, que totalizaram, naquele ano, 60 000 casos.
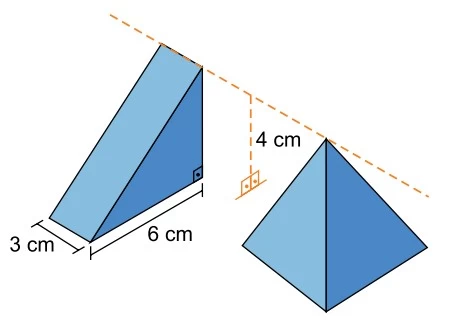
A figura indica um prisma reto triangular e uma pirâmide - FAMERP 2018
Matemática - 2018A figura indica um prisma reto triangular e uma pirâmide regular de base quadrada. A altura desses sólidos, em relação ao plano em que ambos estão apoiados, é igual a 4 cm, como indicam as figuras.
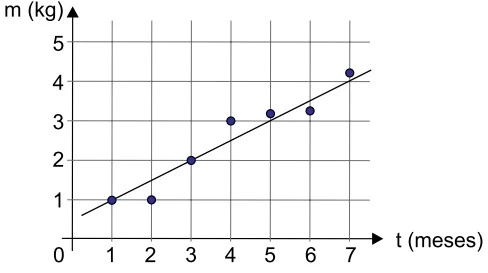
Um animal, submetido à ação de uma droga experimental - FAMERP 2018
Matemática - 2018Um animal, submetido à ação de uma droga experimental, teve sua massa corporal registrada nos sete primeiros meses de vida. Os sete pontos destacados no gráfico mostram esses registros e a reta indica a tendência de evolução da massa corporal em animais que não tenham sido submetidos à ação da droga experimental. Sabe-se que houve correlação perfeita entre os registros coletados no experimento e a reta apenas no 1.° e no 3.° mês.
Sendo x um número inteiro, a mediana do conjunto - FAMERP 2018
Matemática - 2018Sendo x um número inteiro, a mediana do conjunto {3, 7, 2, –3, 13, 9, –1, x} de oito números é igual a 7/2.
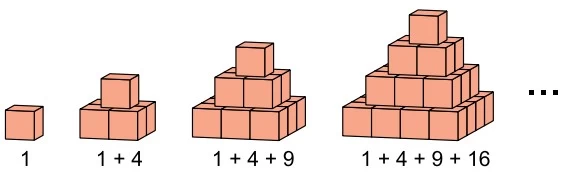
As figuras indicam uma sequência de empilhamentos de - FAMERP 2018
Matemática - 2018As figuras indicam uma sequência de empilhamentos de cubos de 1 cm3. Da primeira pilha em diante, os volumes das pilhas, em cm3, são iguais a 1, 5, 14, 30, 55, e assim sucessivamente.
Lucas possui 6 livros diferentes e Milton possui 8 - FAMERP 2018
Matemática - 2018Lucas possui 6 livros diferentes e Milton possui 8 revistas diferentes. Os dois pretendem fazer uma troca de 3 livros por 3 revistas.
Sabendo-se que uma das raízes da equação algébrica 2x3 - FAMERP 2018
Matemática - 2018Sabendo-se que uma das raízes da equação algébrica 2x3 – 3x2 – 72x – 35 = 0 é 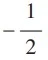 , a soma das outras duas raízes é igual a
, a soma das outras duas raízes é igual a
Um granjeiro tem estoque de ração para alimentar 420 - FAMERP 2018
Matemática - 2018Um granjeiro tem estoque de ração para alimentar 420 galinhas por 80 dias. Depois de x dias de uso desse estoque, o granjeiro vendeu 70 das 420 galinhas. Com a venda, o restante do estoque de ração durou 12 dias a mais do que esse restante de ração duraria se ele não tivesse vendido as galinhas.
As tomografias computadorizadas envolvem sobreposição - FAMERP 2018
Matemática - 2018As tomografias computadorizadas envolvem sobreposição de imagens e, em algumas situações, é necessário conhecer a área da região de intersecção das imagens sobrepostas. Na figura, um triângulo equilátero ABC se sobrepõe a um círculo de centro N e raio NB = NC = NM, com M e N sendo pontos médios, respectivamente, de 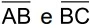
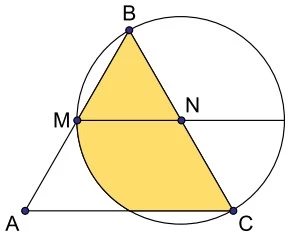
Observe os gráficos das funções reais f e g, definidas - FAMERP 2018
Matemática - 2018Observe os gráficos das funções reais f e g, definidas por f(x) = 2sen x e g(x) = 4cos x.
O ibuprofeno é uma medicação prescrita para dor e febre - UNESP 2018
Matemática - 2018O ibuprofeno é uma medicação prescrita para dor e febre, com meia-vida de aproximadamente 2 horas. Isso significa que, por exemplo, depois de 2 horas da ingestão de 200 mg de ibuprofeno, permanecerão na corrente sanguínea do paciente apenas 100 mg da medicação. Após mais 2 horas (4 horas no total), apenas 50 mg permanecerão na corrente sanguínea e, assim, sucessivamente.
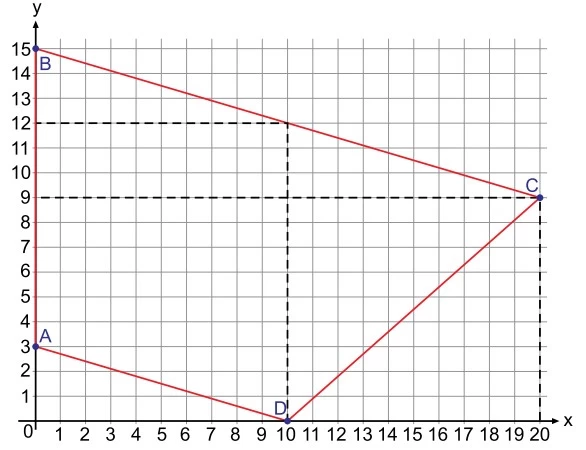
A figura indica um trapézio ABCD no plano cartesiano. - UNESP 2018
Matemática - 2018A figura indica um trapézio ABCD no plano cartesiano.
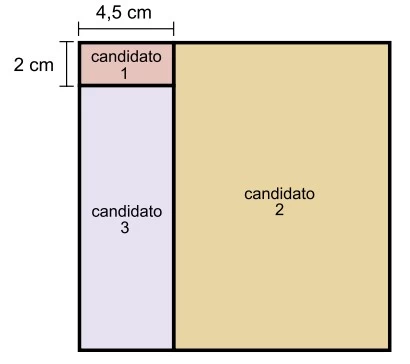
Os estudantes 1, 2 e 3 concorreram a um mesmo cargo da - UNESP 2018
Matemática - 2018Os estudantes 1, 2 e 3 concorreram a um mesmo cargo da diretoria do grêmio de uma faculdade da UNESP, sendo que 1 obteve 6,25% do total de votos que os três receberam para esse cargo. Na figura, a área de cada um dos três retângulos representa a porcentagem de votos obtidos pelo candidato correspondente. Juntos, os retângulos compõem um quadrado, cuja área representa o total dos votos recebidos pelos três candidatos.
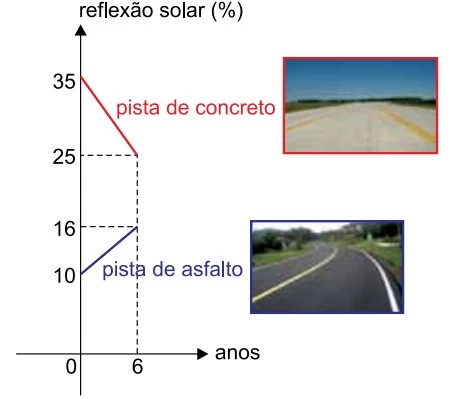
Dois dos materiais mais utilizados para fazer pistas de - UNESP 2018
Matemática - 2018Dois dos materiais mais utilizados para fazer pistas de rodagem de veículos são o concreto e o asfalto. Uma pista nova de concreto reflete mais os raios solares do que uma pista nova de asfalto; porém, com os anos de uso, ambas tendem a refletir a mesma porcentagem de raios solares, conforme mostram os segmentos de retas nos gráficos.
A sequência de figuras, desenhadas em uma malha - UNESP 2018
Matemática - 2018A sequência de figuras, desenhadas em uma malha quadriculada, indica as três primeiras etapas de formação de um fractal. Cada quadradinho dessa malha tem área de 1 cm2.
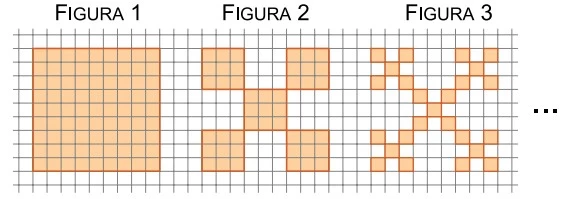
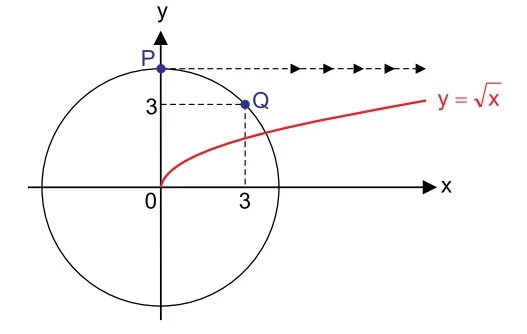
Os pontos P e Q(3, 3) pertencem a uma circunferência - UNESP 2018
Matemática - 2018Os pontos P e Q(3, 3) pertencem a uma circunferência centrada na origem do plano cartesiano. P também é ponto de intersecção da circunferência com o eixo y.
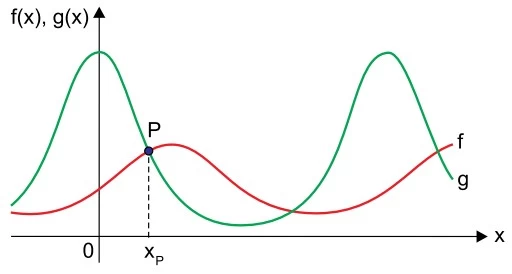
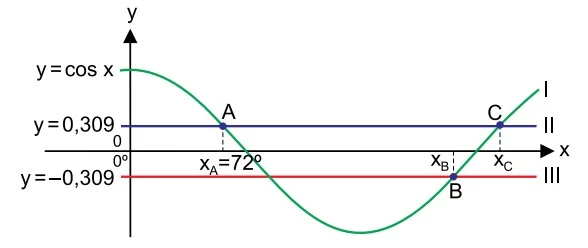
A figura indica os gráficos das funções I, II e III. Os - UNESP 2018
Matemática - 2018A figura indica os gráficos das funções I, II e III. Os pontos A(72º, 0,309), B(xB, – 0,309) e C(xC, 0,309) são alguns dos pontos de intersecção dos gráficos.
Renata escolhe aleatoriamente um número real de – 4 a 2 e - UNESP 2018
Matemática - 2018Renata escolhe aleatoriamente um número real de – 4 a 2 e diferente de zero, denotando-o por x. Na reta real, o intervalo numérico que necessariamente contém o número 2-x/x é
Sejam a e b dois números inteiros positivos. Diz-se que - FUVEST 2017
Matemática - 2017Sejam a e b dois números inteiros positivos. Diz-se que a e b são equivalentes se a soma dos divisores positivos de a coincide com a soma dos divisores positivos de b. Constituem dois inteiros positivos equivalentes:
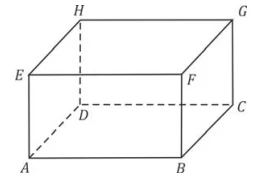
O paralelepípedo retorretângulo ABCDEFGH, representado - FUVEST 2017
Matemática - 2017O paralelepípedo retorretângulo ABCDEFGH, representado na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2.
João tem R$ 150,00 para comprar canetas em 3 lojas. Na - FUVEST 2017
Matemática - 2017João tem R$ 150,00 para comprar canetas em 3 lojas. Na loja A, as canetas são vendidas em dúzias, cada dúzia custa R$ 40,00 e há apenas 2 dúzias em estoque. Na loja B, as canetas são vendidas em pares, cada par custa R$ 7,60 e há 10 pares em estoque. Na loja C, as canetas são vendidas avulsas, cada caneta custa R$ 3,20 e há 25 canetas em estoque. O maior número de canetas que João pode comprar nas lojas A, B e C utilizando no máximo R$ 150,00 é igual a
Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo - FUVEST 2017
Matemática - 2017Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é
O retângulo ABCD, representado na figura, tem lados de - FUVEST 2017
Matemática - 2017O retângulo ABCD, representado na figura, tem lados de comprimento AB = 3 e BC = 4. O ponto P pertence ao lado BC e BP = 1. Os pontos R, S e T, pertencem aos lados AB, CD e AD, respectivamente. O segmento RS é paralelo AD e intercepta DP no ponto Q. O segmento TQ é paralelo a AB.
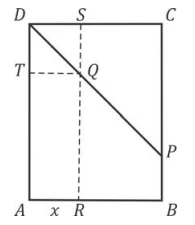
Na figura, o retângulo ABCD tem lados de comprimento AB - FUVEST 2017
Matemática - 2017Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado BC e N o ponto médio do lado CD. Os segmentos AM e AC interceptam o segmento BN nos pontos E e F, respectivamente.
Considere as funções f(x) = x2 + 4 e g(x) = 1 + log 1/2 - FUVEST 2017
Matemática - 2017Considere as funções f(x) = x2 + 4 e g(x) = 1 + log 1/2 x, em que o domínio de f é o conjunto dos números reais e o domínio de g é o conjunto dos números reais maiores do que 0. Seja,
h(x) = 3f(g(x)) + 2g(f(x)), em que x > 0. Então, h(2) é igual a
O polinômio P(x) = x3 – 3x2 + 7x – 5 possui uma raiz - FUVEST 2017
Matemática - 2017O polinômio P(x) = x3 – 3x2 + 7x – 5 possui uma raiz complexa ξ cuja parte imaginária é positiva. A parte real de ξ3 é igual a
Um reservatório de água tem o formato de um cone - FUVEST 2017
Matemática - 2017Um reservatório de água tem o formato de um cone circular reto. O diâmetro de sua base (que está apoiada sobre o chão horizontal) é igual a 8 m. Sua altura é igual a 12 m. A partir de um instante em que o reservatório está completamente vazio, inicia-se seu enchimento com água a uma vazão constante de 500 litros por minuto. O tempo gasto para que o nível de água atinja metade da altura do reservatório é de, aproximadamente,
Duas circunferências com raios 1 e 2 têm centros no - FUVEST 2017
Matemática - 2017Duas circunferências com raios 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x1, y1) e (x2, y2).
O valor de (x1 + y1)2 + (x2 + y2)2 é igual a
Uma quantidade fixa de um gás ideal é mantida a - FUVEST 2017
Matemática - 2017Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
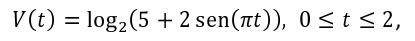
em que t é medido em horas e V(t) é medido em m3. A pressão máxima do gás no intervalo de tempo [0, 2] ocorre no instante
Uma confeitaria vendeu seus dois últimos bolos por - UNESP 2017/2
Matemática - 2017Uma confeitaria vendeu seus dois últimos bolos por R$ 32,00 cada. Ela teve lucro de 28% com a venda de um dos bolos, e prejuízo de 20% com a venda do outro.
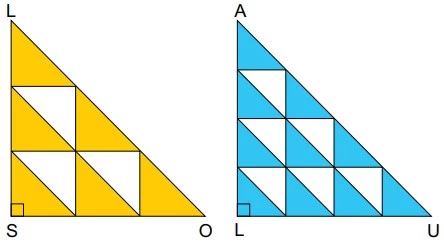
Os polígonos SOL e LUA são triângulos retângulos - UNESP 2017/2
Matemática - 2017Os polígonos SOL e LUA são triângulos retângulos isósceles congruentes. Os triângulos retângulos brancos no interior de SOL são congruentes, assim como também são congruentes os triângulos retângulos brancos no interior de LUA.
Um grupo de estudantes fará uma excursão e alugará - UNESP 2017/2
Matemática - 2017Um grupo de estudantes fará uma excursão e alugará ônibus para transportá-lo. A transportadora dispõe de ônibus em dois tamanhos, pequeno e grande. O pequeno tem capacidade para 24 pessoas, ao custo total de R$ 500,00. O grande tem capacidade para 40 pessoas, ao custo total de R$ 800,00. Sabe-se que pelo menos 120 estudantes participarão da excursão e que o grupo não quer gastar mais do que R$ 4.000,00 com o aluguel dos ônibus.
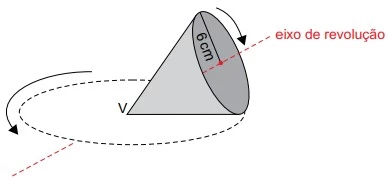
Um cone circular reto, de vértice V e raio da base - UNESP 2017/2
Matemática - 2017Um cone circular reto, de vértice V e raio da base igual a 6 cm, encontra-se apoiado em uma superfície plana e horizontal sobre uma geratriz. O cone gira sob seu eixo de revolução que passa por V, deslocando-se sobre a superfície plana horizontal, sem escorregar, conforme mostra a figura.
Uma função quadrática f é dada por f(x) = x2 + bx + c - UNESP 2017/2
Matemática - 2017Uma função quadrática f é dada por f(x) = x2 + bx + c, com b e c reais. Se f(1) = –1 e f(2) – f(3) = 1, o menor valor que f(x) pode assumir, quando x varia no conjunto dos números reais, é igual a
Admita que o número de visitas diárias a um site seja - UNESP 2017/2
Matemática - 2017Admita que o número de visitas diárias a um site seja expresso pela potência 4n, com n sendo o índice de visitas ao site. Se o site S possui o dobro do número de visitas diárias do que um site que tem índice de visitas igual a 6, o índice de visitas ao site S é igual a
Uma criança possui 6 blocos de encaixe, sendo 2 - UNESP 2017/2
Matemática - 2017Uma criança possui 6 blocos de encaixe, sendo 2 amarelos, 2 vermelhos, 1 verde e 1 azul.
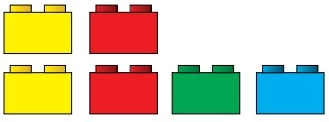
Usando essas peças, é possível fazer diferentes pilhas de três blocos. A seguir, são exemplificadas quatro das pilhas possíveis.
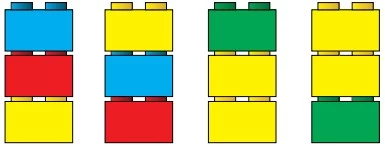
As torneiras A, B e C, que operam com vazão constante, pode - FGV 2017
Matemática - 2017As torneiras A, B e C, que operam com vazão constante, podem, cada uma, encher um reservatório vazio em 60 horas, 48 horas e 80 horas, respectivamente. Para encher esse mesmo reservatório vazio, inicialmente abre-se a torneira A por quatro horas e, em seguida, fecha-se a torneira A e abre-se a torneira B por quatro horas. Por fim, fecha-se a torneira B e abre-se a torneira C até que o reservatório se encha por completo.
A conta armada a seguir indica a adição de três números - FGV 2017
Matemática - 2017A conta armada a seguir indica a adição de três números naturais, cada um com três algarismos, resultando em um número natural de quatro algarismos. Os algarismos que compõem os números envolvidos na conta, indicados pelas letras A, C, D e E, representam números primos distintos entre si.

As cidades A, B, C e D estão ligadas por uma rodovia, como - FGV 2016
Matemática - 2017As cidades A, B, C e D estão ligadas por uma rodovia, como mostra a figura seguinte, feita fora de escala.
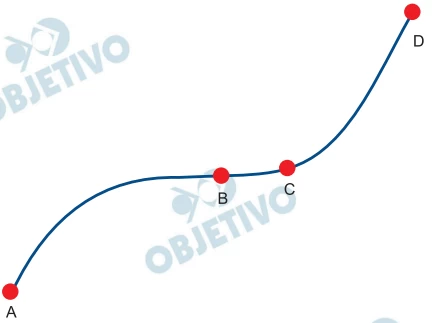
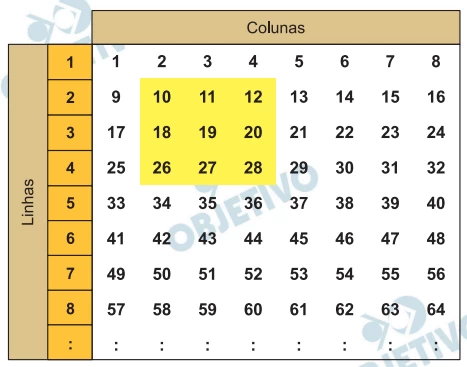
Na tabela de 8 colunas e infinitas linhas numeradas, indica - FGV 2017
Matemática - 2017Na tabela de 8 colunas e infinitas linhas numeradas, indicada na figura, podemos formar infinitos quadrados coloridos 3x3, como mostra um exemplo.
Removendo um número do conjunto {11, 12, 17, 18, 23, 29, 30 - FGV 2017
Matemática - 2017Removendo um número do conjunto {11, 12, 17, 18, 23, 29, 30} formamos um novo conjunto com média aritmética dos elementos igual a 18,5.
Em uma prova de matemática de 10 questões, cada questão - FGV 2017
Matemática - 2017Em uma prova de matemática de 10 questões, cada questão vale zero ou um ponto, não havendo pontuações intermediárias.
Concede-se conceito C para os alunos que fizerem de 5 a 6 pontos, conceito B para os que fizerem de 7 a 8 pontos, e A para os que fizerem de 9 a 10 pontos. Alunos que fizerem menos do que 5 pontos recebem conceito insatisfatório.
A torre de controle de tráfego marítimo de Algés, em - FGV 2017
Matemática - 2017A torre de controle de tráfego marítimo de Algés, em Portugal, tem o formato de um prisma oblíquo, com base retangular de área 247 m2. A inclinação da torre é de aproximadamente 76,7°, com deslocamento horizontal de 9 m da base superior em relação à base inferior do prisma.

Os pontos de coordenadas cartesianas (2, 3) e (–1, 2) - FGV 2017
Matemática - 2017Os pontos de coordenadas cartesianas (2, 3) e (–1, 2) pertencem a uma circunferência.
Para certos valores reais de k, o polinômio P(x) = x2 – 6x - FGV 2017
Matemática - 2017Para certos valores reais de k, o polinômio P(x) = x2 – 6x +| 2k – 7 | é divisível por x–1.
Suponha que fosse possível dar uma volta completa em torno - FGV 2017
Matemática - 2017Suponha que fosse possível dar uma volta completa em torno da linha do Equador caminhando e que essa linha fosse uma circunferência perfeita na esfera terrestre.
O índice de Angstrom (IA), usado para alertas de risco de - FGV 2017
Matemática - 2017O índice de Angstrom (IA), usado para alertas de risco de incêndio, é uma função da umidade relativa do ar (U), em porcentagem, e da temperatura do ar (T), em °C. O índice é calculado pela fórmula 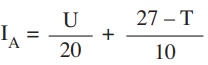 e sua interpretação feita por meio da tabela a seguir
e sua interpretação feita por meio da tabela a seguir

Um estudante de Economia precisa escolher exatamente duas - FGV 2017
Matemática - 2017Um estudante de Economia precisa escolher exatamente duas dentre três disciplinas eletivas, que são: econometria, microeconomia, macroeconomia. A probabilidade de ele escolher econometria é a mesma que a de ele escolher microeconomia, cada uma igual a 62,5%.
Uma fração, definida como a razão entre dois inteiros, - FGV 2017
Matemática - 2017Uma fração, definida como a razão entre dois inteiros, chama-se imprópria quando o numerador é maior ou igual ao denominador e chama-se decimal quando o denominador é uma potência de dez.
Os pontos A(0, 1), B(1, 1), C(1, 0) e D(–k, –k), com k > 0, - FGV 2017
Matemática - 2017Os pontos A(0, 1), B(1, 1), C(1, 0) e D(–k, –k), com k; 0, formam o quadrilátero convexo ABCD, com eixo de simetria BD sobre a bissetriz dos quadrantes ímpares.

A equação algébrica x3 – 7x2 + kx + 216 = 0, em que k é um - FGV 2017
Matemática - 2017A equação algébrica x3 – 7x2 + kx + 216 = 0, em que k é um número real, possui três raízes reais.
Apoie nosso trabalho!
Assine Agora