Matemática
Exibindo questões de 801 a 888.
Uma impressora deveria imprimir todos os números inteiros - FGV 2014
Matemática - 2014Uma impressora deveria imprimir todos os números inteiros de 1 até 225, em ordem crescente e um de cada vez. A tinta da impressora acabou antes que o serviço fosse completado, tendo deixado de imprimir um total de 452 algarismos.
Três das arestas de um cubo, com um vértice em comum, - FUVEST 2014
Matemática - 2014Três das arestas de um cubo, com um vértice em comum, são também arestas de um tetraedro. A razão entre o volume do tetraedro e o volume do cubo é
Na reta real, os pontos P e Q correspondem, respectivamente - FGV 2014
Matemática - 2014Na reta real, os pontos P e Q correspondem, respectivamente, aos números –5 e 3. R e S são pontos distintos nessa mesma reta, e a distância de cada um deles até o ponto P é igual ao dobro da distância deles até o ponto Q.
O total de x moedas convencionais (cara e coroa nas faces) - FGV 2014
Matemática - 2014O total de x moedas convencionais (cara e coroa nas faces) estão sobre uma mesa. Dessas moedas 1/5, está em posição de coroa, ou seja, com a face coroa voltada para cima. Se invertermos o lado de 3 moedas que estão em posição de cara1/4, das moedas ficará em posição de coroa.
Se o sétimo termo de uma progressão geométrica de termos - FGV 2014
Matemática - 2014Se o sétimo termo de uma progressão geométrica de termos positivos é 20, e o décimo terceiro termo é 11,
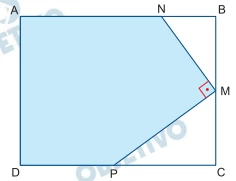
A figura indica um retângulo ABCD, com AB = 10 cm e AD = 6 - FGV 2014
Matemática - 2014A figura indica um retângulo ABCD, com AB = 10 cm e AD = 6 cm. Os pontos M, N e P estão nos lados do retângulo, sendo que M é ponto médio de BC, e AN = 8 cm.
Os números naturais ímpares foram dispostos em um arranjo - FGV 2014
Matemática - 2014Os números naturais ímpares foram dispostos em um arranjo triangular, como indica a figura.
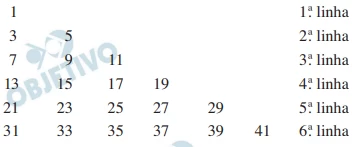
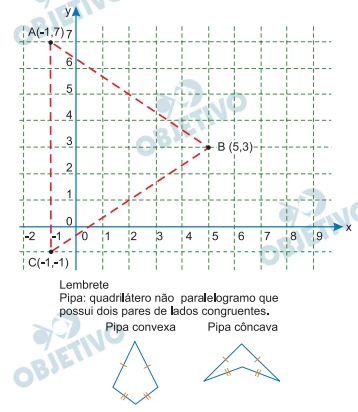
No interior e no exterior do triângulo ABC, com dados - FGV 2014
Matemática - 2014No interior e no exterior do triângulo ABC, com dados indicados na figura, serão marcados os pontos distintos P’ e P”. Ligando-se convenientemente cada um desses pontos com os vértices do triângulo ABC, os polígonos obtidos serão pipas côncavas de área 16.
13 A A atual moeda de 1 real é composta de aço inox no - FGV 2014
Matemática - 2014A atual moeda de 1 real é composta de aço inox no círculo central e de aço inox revestido de bronze na coroa circular. Essa moeda possui diâmetro e espessura aproximados de 26 e 2 milímetros, respectivamente. Uma corda no círculo dessa moeda que seja tangente ao círculo central de aço inox mede, aproximadamente, 18 milímetros.
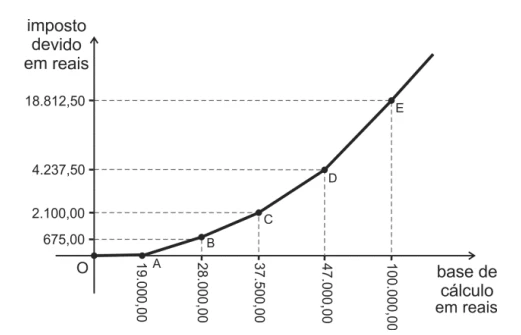
Seja k um número real tal que os gráficos das funções reais - FGV 2014
Matemática - 2014Seja k um número real tal que os gráficos das funções reais dadas por y = |x| e y = –|x|+ k delimitem um polígono de área 16.
Admita que (A, B, C, D, E, F) seja uma sêxtupla ordenada de - FGV 2014
Matemática - 2014Admita que (A, B, C, D, E, F) seja uma sêxtupla ordenada de números inteiros maiores ou iguais a 1 tais que A ≤ B ≤ C ≤ D ≤ E ≤ F.
A respeito dos números que compõem essa sêxtupla, sabe-se que:
a mediana e a moda da sequência A, B, C, D, E, F são, ambas, iguais a 2;
a diferença entre F e A é 19.
Se a soma dos inversos das raízes reais da equação - FUVEST 2023
Matemática - 2014Se a soma dos inversos das raízes reais da equação polinomial x2 – 2kx + 36 = 0, em que k é uma constante
Existem três possibilidades de rota (A, B e C) para a - FGV 2014
Matemática - 2014Existem três possibilidades de rota (A, B e C) para a construção de uma nova linha do metrô. De acordo com estudos iniciais de viabilidade, a probabilidade de que a rota B seja escolhida é 10% maior do que a probabilidade de que a rota C seja escolhida. Os mesmos estudos revelam que a probabilidade de que a rota C seja escolhida é 20% maior do que a probabilidade de que rota A seja escolhida.
O conjunto solução da equação (x2 – 14)2 · (3y – 9)3 = 108, - FGV 2014
Matemática - 2014O conjunto solução da equação (x2 – 14)2 · (3y – 9)3 = 108, com x e y inteiros, possui n pares ordenados (x, y).
Com relação ao polinômio de coeficientes reais dado por - FGV 2014
Matemática - 2014Com relação ao polinômio de coeficientes reais dado por P(x) = x4 + ax3 + bx2 + cx + d, sabe-se que P(2i) = P(2 + i) = 0, com i2 = –1.
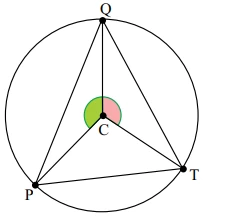
O triângulo PQT, indicado na figura, está inscrito em uma - FGV 2014
Matemática - 2014O triângulo PQT, indicado na figura, está inscrito em uma circunferência de centro C, sendo que as medidas dos ângulos PCˆQ e TCˆQ são, respectivamente, iguais a α e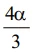
No desenvolvimento do binômio 7 1 2 Ax 2 x- FGV 2014
Matemática - 2014No desenvolvimento do binômio 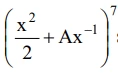 segundo a ordem decrescente de seus expoentes, o quinto termo é igual a
segundo a ordem decrescente de seus expoentes, o quinto termo é igual a 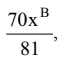 com A e B constantes racionais.
com A e B constantes racionais.
Um semáforo de trânsito está regulado de forma que a luz - FGV 2014
Matemática - 2014Um semáforo de trânsito está regulado de forma que a luz verde fica acesa por 30 segundos, em seguida se acende a luz amarela por 3 segundos, e depois a luz vermelha por 30 segundos.
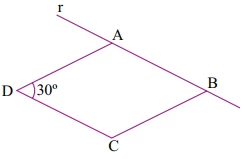
O losango ABCD, indicado na figura, tem lado de medida 6 cm - FGV 2014
Matemática - 2014O losango ABCD, indicado na figura, tem lado de medida 6 cm. Esse losango será rotacionado em 360° em torno de uma reta r que contém seu lado AB.
Renato participou de uma sequência de seis apostas - FGV 2014
Matemática - 2014Renato participou de uma sequência de seis apostas consecutivas. Em cada aposta, ele arriscou ganhar ou perder metade do valor apostado. Renato começou apostando R$ 100,00 e, durante as demais apostas, sempre apostou todo o saldo do dinheiro que tinha ao final da aposta anterior. Sabe-se que Renato ganhou três e perdeu três das seis apostas.
Os pontos P e Q estão em uma semicircunferência de centro C - FGV 2014
Matemática - 2014Os pontos P e Q estão em uma semicircunferência de centro C e diâmetro AB, formando com A o triângulo APQ, conforme indica a figura.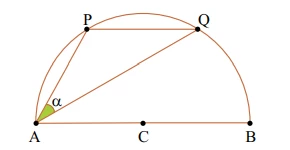
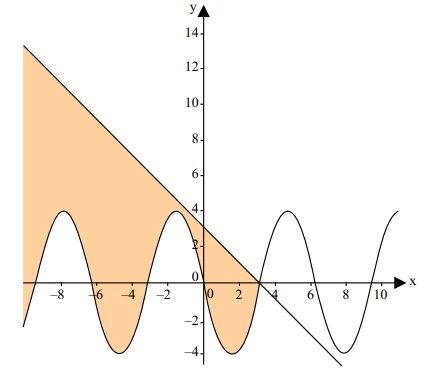
No gráfico, observam-se uma senoide de equação y = –4 sen x - FGV 2014
Matemática - 2014No gráfico, observam-se uma senoide de equação y = –4 sen x e uma reta de coeficiente angular igual a –1, que intersecta a senoide e o eixo x no mesmo ponto do plano cartesiano.
Em uma urna, temos 32 objetos, que são: 8 dados brancos, 8 - FGV 2014
Matemática - 2014Em uma urna, temos 32 objetos, que são: 8 dados brancos, 8 dados pretos, 8 esferas brancas e 8 esferas pretas.
Investindo certo capital a juros compostos de k% ao mês, o - FGV 2014
Matemática - 2014Investindo certo capital a juros compostos de k% ao mês, o capital investido será acrescido em 60% no período de 5 meses. Consultando dados do gráfico a seguir,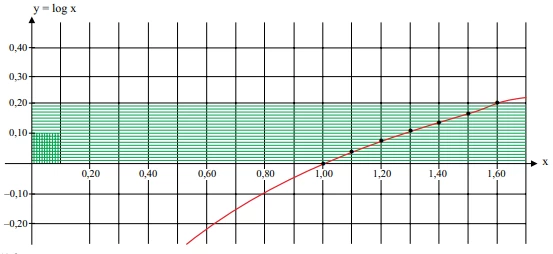
- FGV 2014
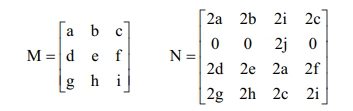
Matemática - 2014Sejam M3x3 e N4x4 as matrizes quadradas indicadas a seguir, com a, b, c, d, e, f, g, h, i, j sendo números reais.
Em certa região do litoral paulista, o preço do metro - FGV 2014
Matemática - 2014Em certa região do litoral paulista, o preço do metro quadrado de terreno é R$ 400,00. O Sr. Joaquim possui um terreno retangular com 78 metros de perímetro, sendo que a diferença entre a medida do lado maior e a do menor é 22 metros.
Toda segunda-feira, Valéria coloca R$ 100,00 de gasolina no - FGV 2014
Matemática - 2014Toda segunda-feira, Valéria coloca R$ 100,00 de gasolina no tanque de seu carro. Em uma determinada segunda-feira, o preço por litro do combustível sofreu um acréscimo de 5% em relação ao preço da segunda-feira anterior. Nessas condições, na última segunda-feira, o volume de gasolina colocado foi x% inferior ao da segunda-feira anterior.
Uma fábrica de panelas opera com um custo fixo mensal de R$ - FGV 2014
Matemática - 2014Uma fábrica de panelas opera com um custo fixo mensal de R$ 9 800,00 e um custo variável por panela de R$ 45,00. Cada panela é vendida por R$ 65,00. Seja x a quantidade que deve ser produzida e vendida mensalmente para que o lucro mensal seja igual a 20% da receita.
No plano cartesiano, há dois pontos R e S pertencentes à - FGV 2014
Matemática - 2014No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação y = x2 e que estão alinhados com os pontos A(0,3) e B(4,0).
No plano cartesiano, uma circunferência tem centro C(5,3) e - FGV 2014
Matemática - 2014No plano cartesiano, uma circunferência tem centro C(5,3) e tangencia a reta de equação 3x + 4y - 12 = 0.
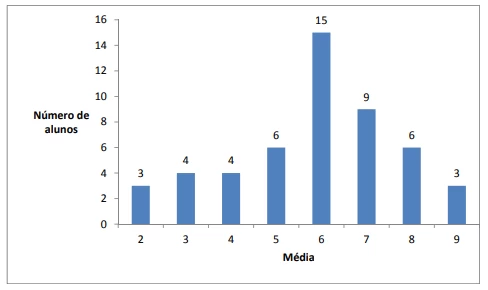
A média mínima para um aluno ser aprovado em certa - FGV 2014
Matemática - 2014A média mínima para um aluno ser aprovado em certa disciplina de uma escola é 6. A distribuição de frequências das médias dos alunos de uma classe, nessa disciplina, é dada abaixo:
Uma senha de internet é constituída de seis letras e quatro - FGV 2014
Matemática - 2014Uma senha de internet é constituída de seis letras e quatro algarismos em que a ordem é levada em consideração. Eis uma senha possível: (a,a,b,7,7,b,a,7,a,7)
Dos animais de uma fazenda, 40% são bois, 30% vacas, e os - FGV 2015
Matemática - 2014Dos animais de uma fazenda, 40% são bois, 30% vacas, e os demais são caprinos. Se o dono da fazenda vende 30% dos bois e 70% das vacas,
Dois eventos A e B de um espaço amostral são independentes. - FGV 2014
Matemática - 2014Dois eventos A e B de um espaço amostral são independentes. A probabilidade do evento A é P( A) = 0,4 e a probabilidade da união de A com B é P( AuB ) = 0,8 .
Três números estão em progressão geométrica de razão - FGV 2014
Matemática - 2014Três números estão em progressão geométrica de razão 3/2 Diminuindo 5 unidades do terceiro número da progressão, ela se transforma em uma progressão aritmética.
Considere a aproximação: log 2 = 0,3. É correto afirmar que - FGV 2014
Matemática - 2014Considere a aproximação: log 2 = 0,3.
Três sócios A, B e C resolvem abrir uma sociedade com um - FGV 2014
Matemática - 2014Três sócios A, B e C resolvem abrir uma sociedade com um capital de R$ 100 000,00.
Uma piscina vazia, com formato de paralelepípedo reto - FGV 2024
Matemática - 2014Uma piscina vazia, com formato de paralelepípedo reto retângulo, tem comprimento de 10m, largura igual a 5m e altura de 2m. Ela é preenchida com água a uma vazão de 5 000 litros por hora.
O número 1 é raiz de multiplicidade 2 da equação polinomial - FGV 2014
Matemática - 2014O número 1 é raiz de multiplicidade 2 da equação polinomial x4 – 2x3 – 3x2 + ax + b = 0.
A figura representa um trapézio isósceles ABCD, com AD = BC - FGV 2015
Matemática - 2014A figura representa um trapézio isósceles ABCD, com AD = BC = 4 cm. M é o ponto médio de 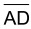 e o ângulo BMC é reto.
e o ângulo BMC é reto.
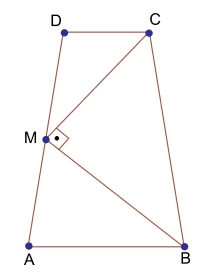
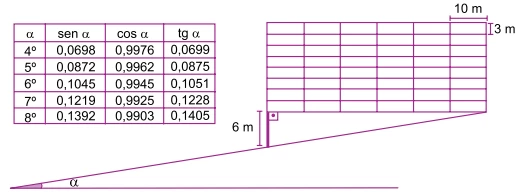
Um edifício comercial tem 48 salas, distribuídas em 8 - FGV 2015
Matemática - 2014Um edifício comercial tem 48 salas, distribuídas em 8 andares, conforme indica a figura. O edifício foi feito em um terreno cuja inclinação em relação à horizontal mede α graus. A altura de cada sala é 3 m, a extensão 10 m, e a altura da pilastra de sustentação, que mantém o edifício na horizontal, é 6 m.
O gráfico abaixo apresenta a receita semestral (em milhões - FGV 2014
Matemática - 2014O gráfico abaixo apresenta a receita semestral (em milhões de reais) de uma empresa em função do tempo em que I/2012 representa o 1º semestre de 2012, II/2012 representa o 2º semestre de 2012 e assim por diante.
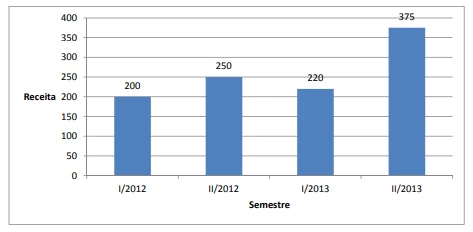
Estima-se que
• a variação porcentual da receita de I/2014 em relação à de I/2013 seja igual à variação porcentual da receita de I/2013 em relação à de I/2012;
• a variação porcentual da receita de II/2014 em relação à de II/2013 seja igual à variação porcentual da receita de II/2013 em relação à de II/2012.
No plano cartesiano, qual dos pontos abaixo é exterior à - FGV 2014
Matemática - 2014No plano cartesiano, qual dos pontos abaixo é exterior à circunferência de equação
Considerando um horizonte de tempo de 10 anos a partir de - FGV 2014
Matemática - 2014Considerando um horizonte de tempo de 10 anos a partir de hoje, o valor de uma máquina deprecia linearmente com o tempo, isto é, o valor da máquina y em função do tempo x é dado por uma função polinomial do primeiro grau y = ax + b .
Quantos números inteiros satisfazem a inequação (3x – 25)(5 - FGV 2014
Matemática - 2014Quantos números inteiros satisfazem a inequação
O volume de uma esfera de raio r é dado por V = π r3. Um - FGV 2014
Matemática - 2014O volume de uma esfera de raio r é dado por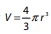 . Um reservatório com formato esférico tem um volume de 36π metros cúbicos.
. Um reservatório com formato esférico tem um volume de 36π metros cúbicos.
Dada a equação polinomial x4 – 3x3 – 8x2 + 22x – 24 = 0 - FGV 2014
Matemática - 2014Dada a equação polinomial x4 – 3x3 – 8x2 + 22x – 24 = 0 e sabendo-se que 1 + i é uma das raízes (i é a unidade imaginária),
Em uma urna há 72 bolas idênticas mas com cores diferentes. - FGV 2014
Matemática - 2014Em uma urna há 72 bolas idênticas mas com cores diferentes. Há bolas brancas, vermelhas e pretas. Ao sortearmos uma bola da urna, a probabilidade de ela ser branca é 1/4 e a probabilidade de ela ser vermelha é 1/3.
Dois triângulos são semelhantes. O perímetro do primeiro é - FGV 2014
Matemática - 2014Dois triângulos são semelhantes. O perímetro do primeiro é 24m e o do segundo é 72m.
Uma televisão é vendida em duas formas de pagamento: • Em - FGV 2014
Matemática - 2014Uma televisão é vendida em duas formas de pagamento:
• Em uma única prestação de R$ 2 030,00, um mês após a compra.
• Entrada de R$ 400,00 mais umas prestação de R$ 1 600,00, um mês após a compra.
As prestações de um financiamento imobiliário constituem - FGV 2014
Matemática - 2014As prestações de um financiamento imobiliário constituem uma progressão aritmética na ordem em que são pagas.
Sabendo que x pertence ao 2º quadrante e que senx = 0,8, - FGV 2014
Matemática - 2014Sabendo que x pertence ao 2º quadrante e que senx = 0,8,
Considere a seguinte tabela, em que ln(x) representa o - FGV 2014
Matemática - 2014Considere a seguinte tabela, em que ln(x) representa o logaritmo neperiano de x:

No plano cartesiano, a reta (r) de equação y + kx = 2 é - FGV 2014
Matemática - 2014No plano cartesiano, a reta (r) de equação y + kx = 2 é perpendicular à reta (s) que passa pela origem e pelo ponto (−5 1), .
Sejam as matrizes A = e B = [5 8]. A matriz X que satisfaz - FGV 2014
Matemática - 2014Sejam as matrizes 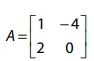 e B =[5 8].
e B =[5 8].
As notas de cem alunos em uma prova foram colocadas em - FGV 2014
Matemática - 2014As notas de cem alunos em uma prova foram colocadas em ordem crescente, originando a sequência de notas (n1, n2, n3, … n100). Sabe-se que
• n1 = 0 e n100 = 9,6
• podem existir notas iguais;
• n50 ≠ n51
Vinte times de futebol disputam a Série A do Campeonato - FUVEST 2013
Matemática - 2013Vinte times de futebol disputam a Série A do Campeonato Brasileiro, sendo seis deles paulistas.
Cada time joga duas vezes contra cada um dos seus adversários. A porcentagem de jogos nos quais os dois oponentes são paulistas é
São dados, no plano cartesiano, o ponto P de coordenadas - FUVEST 2013
Matemática - 2013São dados, no plano cartesiano, o ponto P de coordenadas (3, 6) e a circunferência C de equação (x – 1)2 + (y – 2)2 = 1. Uma reta t passa por P e é tangente a C em um ponto Q. Então a distância de P a Q é
Os vértices de um tetraedro regular são também vértices - FUVEST 2013
Matemática - 2013Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é
As propriedades aritméticas e as relativas à noção de - FUVEST 2013
Matemática - 2013As propriedades aritméticas e as relativas à noção de ordem desempenham um importante papel no estudo dos números reais. Nesse contexto, qual das afirmações abaixo é correta?
Sejam α e β números reais com – π/2 < α < π/2 e 0 < β - FUVEST 2013
Matemática - 2013Sejam α e β números reais com – π/2 < α < π/2 e 0 < β < π. Se o sistema de equações, dado em notação matricial,
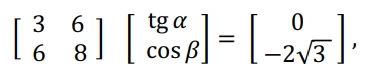
for satisfeito, então α + β é igual a
Quando se divide o Produto Interno Bruto (PIB) de um - FUVEST 2013
Matemática - 2013Quando se divide o Produto Interno Bruto (PIB) de um país pela sua população, obtém-se a renda per capita desse país. Suponha que a população de um país cresça à taxa constante de 2% ao ano. Para que sua renda per capita dobre em 20 anos, o PIB deve crescer anualmente à taxa constante de, aproximadamente,
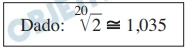
O mapa de uma região utiliza a escala de 1: 200 000. A - FUVEST 2013
Matemática - 2013O mapa de uma região utiliza a escala de 1: 200 000. A porção desse mapa, contendo uma Área de Preservação Permanente (APP), está representada na figura, na qual AF e DF são segmentos de reta, o ponto G está no segmento AF, o ponto E está no segmento DF, ABEG é um retângulo e BCDE é um trapézio.
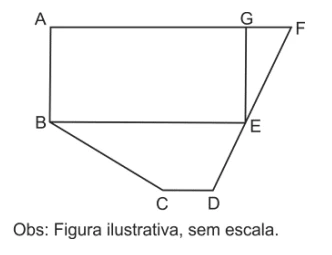
Seja f uma função a valores reais, com domínio D , tal - FUVEST 2013
Matemática - 2013Seja f uma função a valores reais, com domínio D , tal que f(x) = log10(log1/3(x2 – x + 1)), para todo x ∈ D
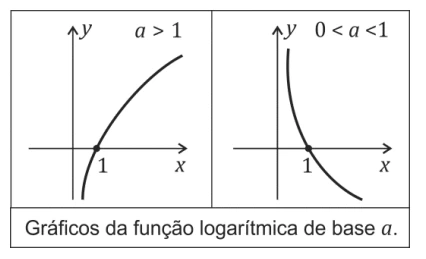
O imposto de renda devido por uma pessoa física à - FUVEST 2013
Matemática - 2013O imposto de renda devido por uma pessoa física à Receita Federal é função da chamada base de cálculo, que se calcula subtraindo o valor das deduções do valor dos rendimentos tributáveis. O gráfico dessa função, representado na figura, é a união dos segmentos de reta OA, AB, BC, CD e da semirreta DE. João preparou sua declaração tendo apurado como base de cálculo o valor de R$ 43.800,00. Pouco antes de enviar a declaração, ele encontrou um documento esquecido numa gaveta que com provava uma renda tributável adicional de R$ 1.000,00. Ao corrigir a declaração, informando essa renda adicional, o valor do imposto devido será acrescido de
Um caminhão sobe uma ladeira com inclinação de 15º. A - FUVEST 2013
Matemática - 2013Um caminhão sobe uma ladeira com inclinação de 15º. A diferença entre a altura final e a altura inicial de um ponto determinado do caminhão, depois de percorridos 100 m da ladeira, será de, aproximadamente,
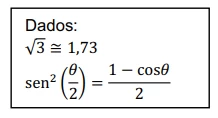
A tabela informa a extensão territorial e a população de - FUVEST 2013
Matemática - 2013A tabela informa a extensão territorial e a população de cada uma das regiões do Brasil, segundo o IBGE.
De uma urna contendo 20 bolas, numeradas de 1 a 20, retira-se uma bola
Matemática - 2013De uma urna contendo 20 bolas, numeradas de 1 a 20, retira-se uma bola.
Em uma festa com n pessoas, em um dado instante, 31 - FUVEST 2012
Matemática - 2012Em uma festa com n pessoas, em um dado instante, 31 mulheres se retiraram e restaram convidados na razão de 2 homens para cada mulher.
Um pouco mais tarde, 55 homens se retiraram e restaram, a seguir, convidados na razão de 3 mulheres para cada homem. O número n de pessoas presentes inicialmente na festa era igual a
O segmento AB é lado de um hexágono regular de área - FUVEST 2012
Matemática - 2012O segmento AB é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de AB de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento AB é igual a
O número real x, com 0 < x < π, satisfaz a equação log3 - FUVEST 2012
Matemática - 2012O número real x, com 0 < x < π, satisfaz a equação log3(1 – cos x) + log3(1 + cos x) = – 2.
Então, cos 2x + sen x vale
Considere a função f(x) = 1 – 4x / ( x+1 )2, a - FUVEST 2012
Matemática - 2012Considere a função f(x) = 1 – 4x / ( x+1 )2, a qual está definida para x ≠ – 1. Então, para todo x ≠ 1 e x ≠ – 1, o produto f(x)f(– x) é igual a
Em um plano, é dado um polígono convexo de seis lados, - FUVEST 2012
Matemática - 2012Em um plano, é dado um polígono convexo de seis lados, cujas medidas dos ângulos internos, dispostas em ordem crescente, formam uma progressão aritmética. A medida do maior ângulo é igual a 11 vezes a medida do menor. A soma das medidas dos quatro menores ângulos internos desse polígono, em graus, é igual a
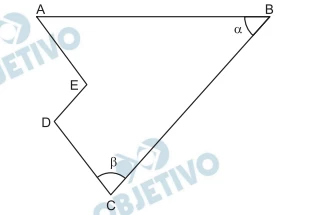
Na figura, tem-se AE paralelo a CD, BC paralelo a DE, AE - FUVEST 2012
Matemática - 2012Na figura, tem-se AE paralelo a CD, BC paralelo a DE, AE = 2, α = 45° e β = 75°. Nessas condições, a distância do ponto E ao segmento AB é igual a
Considere a matriz A = , em que a é um número real. - FUVEST 2012
Matemática - 2012Considere a matriz

No plano cartesiano Oxy, a circunferência C é tangente - FUVEST 2012
Matemática - 2012No plano cartesiano Oxy, a circunferência C é tangente ao eixo Ox no ponto de abscissa 5 e contém o ponto (1; 2).
Nessas condições, o raio de C vale
Considere todos os pares ordenados de números naturais - FUVEST 2012
Matemática - 2012Considere todos os pares ordenados de números naturais (a; b), em que 11 ≤ a ≤ 22 e 43 ≤ b ≤ 51. Cada um desses pares ordenados está escrito em um cartão diferente. Sorteando-se um desses cartões ao acaso, qual é a probabilidade de que se obtenha um par ordenado (a; b) de tal forma que a fração a/b seja irredutível e com denominador par?
Em um tetraedro regular de lado a, a distância entre os - FUVEST 2012
Matemática - 2012Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a
Uma substância radioativa sofre desintegração ao longo - FUVEST 2012
Matemática - 2012Uma substância radioativa sofre desintegração ao longo do tempo, de acordo com a relação m(t) = c . a–kt, em que a é um número real positivo, t é dado em anos, m(t) é a massa da substância em gramas e c, k são constantes positivas. Sabe-se que m0 gramas dessa substância foram reduzidos a 20% em 10 anos. A que porcentagem de m0 ficará reduzida a massa da substância, em 20 anos?
Francisco deve elaborar uma pesquisa sobre dois - FUVEST 2012
Matemática - 2012Francisco deve elaborar uma pesquisa sobre dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação: aranha, besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, carrapato, escorpião e gafanhoto.
Qual é a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
Suponha que x e y são reais e satisfazem x² + y² = 6x + 6y - 10.
Matemática - 2011Suponha que x e y são reais e satisfazem
x² + y² = 6x + 6y - 10.
As bases de um trapézio têm como suporte as retas de equações
Matemática - 2011As bases de um trapézio têm como suporte as retas de equações x − y −1 = 0 e 3y − 3x + 5 = 0. A altura deste trapézio em cm é:
A função f(x) = (m – 5 )x+1 é decrescente, quando: UEPB 2011
Matemática - 2011A função f(x) = (m – 5 )x+1 é decrescente, quando:
Quantos pássaros serão soltos no décimo quinto dia? - UNESP 2009
Matemática - 2009Um viveiro clandestino com quase trezentos pássaros foi encontrado por autoridades ambientais. Pretende-se soltar esses pássaros seguindo um cronograma, de acordo com uma progressão aritmética, de modo que no primeiro dia sejam soltos cinco pássaros, no segundo dia sete pássaros, no terceiro nove, e assim por diante
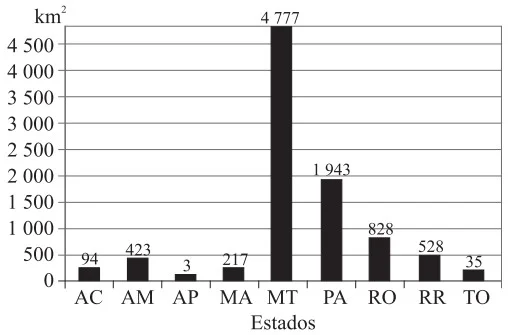
A Amazônia Legal, com área de aproximadamente - UNESP 2009
Matemática - 2009A Amazônia Legal, com área de aproximadamente 5 215 000 km2, compreende os estados do Acre, Amapá, Amazonas, Mato Grosso, Pará, Rondônia, Roraima e Tocantins, e parte do estado do Maranhão. Um sistema de monitoramento e controle mensal do desmatamento da Amazônia utilizado pelo INPE (Instituto Nacional de Pesquisas Espaciais) é o Deter (Detecção de Desmatamento em Tempo Real). O gráfico apresenta dados apontados pelo Deter referentes ao desmatamento na Amazônia Legal, por estado, no período de 1.º de julho de 2007 a 30 de junho de 2008, totalizando 8 848 km2 de área desmatada.
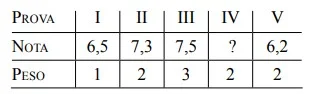
Durante o ano letivo, um professor de matemática - UNESP 2009
Matemática - 2009Durante o ano letivo, um professor de matemática aplicou cinco provas para seus alunos. A tabela apresenta as notas obtidas por um determinado aluno em quatro das cinco provas realizadas e os pesos estabelecidos pelo professor para cada prova.
Numa campanha de preservação do meio ambiente, uma - UNESP 2009
Matemática - 2009Numa campanha de preservação do meio ambiente, uma prefeitura dá descontos na conta de água em troca de latas de alumínio e garrafas de plástico (PET) arrecadadas. Para um quilograma de alumínio, o desconto é de R$ 2,90 na conta de água; para um quilograma de plástico, o abatimento é de R$ 0,17. Uma família obteve R$ 16,20 de desconto na conta de água com a troca de alumínio e garrafas plásticas.
Uma circunferência tem centro (a, b) no primeiro quadrante, raio r e é
Matemática - 2009Uma circunferência tem centro (a, b) no primeiro quadrante, raio r e é tangente aos eixos coordenados. Nessas condições, é correto afirmar:
Apoie nosso trabalho!
Assine Agora