Matemática
Exibindo questões de 301 a 400.
Um biólogo mediu a altura de cinco árvores distintas e - ENEM 2012
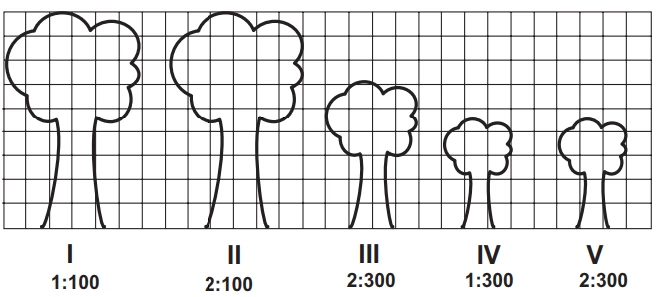
MatemáticaUm biólogo mediu a altura de cinco árvores distintas e representou-as em uma mesma malha quadriculada, utilizando escalas diferentes, conforme indicações na figura a seguir.
O diretor de uma escola convidou os 280 alunos de terceiro - ENEM 2012
MatemáticaO diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
A temperatura T de um forno (em graus centígrados) é - ENEM 2013
MatemáticaA temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão T(t)= - t2 / 4 + 400, com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 ºC.
Na aferição de um novo semáforo, os tempos são ajustados - ENEM 2013
MatemáticaNa aferição de um novo semáforo, os tempos são ajustados de modo que, em cada ciclo completo (verde-amarelo- vermelho), a luz amarela permaneça acesa por 5 segundos, e o tempo em que a luz verde permaneça acesa seja igual a 2/3 do tempo em que a luz vermelha fique acesa. A luz verde fica acesa, em cada ciclo, durante X segundos e cada ciclo dura Y segundos.
Nos Estados Unidos a unidade de medida de volume mais - ENEM 2013
MatemáticaNos Estados Unidos a unidade de medida de volume mais utilizada em latas de refrigerante é a onça fluida (fl oz), que equivale a aproximadamente 2,95 centilitros (cL).
Sabe-se que o centilitro é a centésima parte do litro e que a lata de refrigerante usualmente comercializada no Brasil tem capacidade de 355 mL.
Em setembro de 1987, Goiânia foi palco do maior acidente - ENEM 2013
MatemáticaEm setembro de 1987, Goiânia foi palco do maior acidente radioativo ocorrido no Brasil, quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário para que a massa desse material se reduza à metade. A meia-vida do césio-137 é 30 anos e a quantidade restante de massa de um material radioativo, após t anos, é calculada pela expressão M(t) = A · (2,7)kt, onde A é a massa inicial e k é uma constante negativa.
Considere 0,3 como aproximação para log10 2.
Um artesão de joias tem à sua disposição pedras - ENEM 2013
MatemáticaUm artesão de joias tem à sua disposição pedras brasileiras de três cores: vermelhas, azuis e verdes.
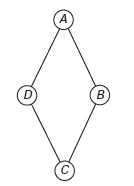
Ele pretende produzir joias constituídas por uma liga metálica, a partir de um molde no formato de um losango não quadrado com pedras nos seus vértices, de modo que dois vértices consecutivos tenham sempre pedras de cores diferentes.
A figura ilustra uma joia, produzida por esse artesão, cujos vértices A, B, C e D correspondem às posições ocupadas pelas pedras.
Um programa de edição de imagens possibilita transformar - ENEM 2013
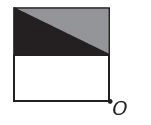
MatemáticaUm programa de edição de imagens possibilita transformar figuras em outras mais complexas. Deseja-se construir uma nova figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O.
Uma torneira não foi fechada corretamente e ficou pingando - ENEM 2013
MatemáticaUma torneira não foi fechada corretamente e ficou pingando, da meia-noite às seis horas da manhã, com a frequência de uma gota a cada três segundos. Sabe-se que cada gota d’agua tem volume de 0,2 mL.
Um banco solicitou aos seus clientes a criação de uma - ENEM 2013
MatemáticaUm banco solicitou aos seus clientes a criação de uma senha pessoal de seis dígitos, formada somente por algarismos de 0 a 9, para acesso à conta corrente pela internet.
Entretanto, um especialista em sistemas de segurança eletrônica recomendou à direção do banco recadastrar seus usuários, solicitando, para cada um deles, a criação de uma nova senha com seis dígitos, permitindo agora o uso das 26 letras do alfabeto, além dos algarismos de 0 a 9. Nesse novo sistema, cada letra maiúscula era considerada distinta de sua versão minúscula. Além disso, era proibido o uso de outros tipos de caracteres.
Uma forma de avaliar uma alteração no sistema de senhas é a verificação do coeficiente de melhora, que é a razão do novo número de possibilidades de senhas em relação ao antigo.
As notas de um professor que participou de um processo - ENEM 2013
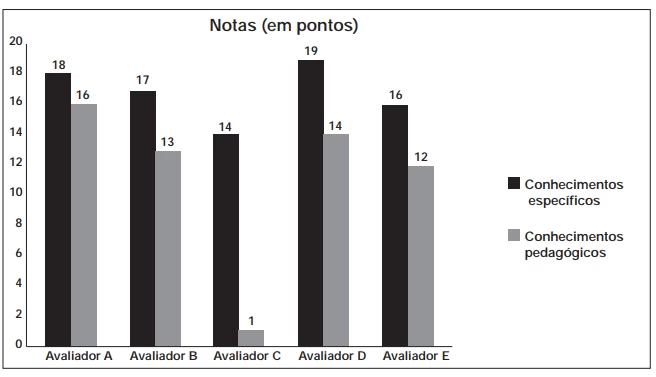
MatemáticaAs notas de um professor que participou de um processo seletivo, em que a banca avaliadora era composta por cinco membros, são apresentadas no gráfico. Sabe-se que cada membro da banca atribuiu duas notas ao professor, uma relativa aos conhecimentos específicos da área de atuação e outra, aos conhecimentos pedagógicos, e que a média final do professor foi dada pela média aritmética de todas as notas atribuídas pela banca avaliadora.
As torres Puerta de Europa são duas torres inclinadas uma - ENEM 2013
MatemáticaAs torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

Numa escola com 1 200 alunos foi realizada uma pesquisa - ENEM 2013
MatemáticaNuma escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras, inglês e espanhol.
Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.
As projeções para a produção de arroz no período de 2012 - ENEM 2013
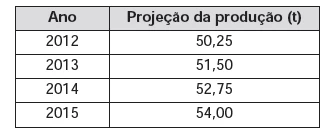
MatemáticaAs projeções para a produção de arroz no período de 2012 – 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
Um dos grandes problemas enfrentados nas rodovias - ENEM 2013
MatemáticaUm dos grandes problemas enfrentados nas rodovias brasileiras é o excesso de carga transportada pelos caminhões. Dimensionado para o tráfego dentro dos limites legais de carga, o piso das estradas se deteriora com o peso excessivo dos caminhões. Além disso, o excesso de carga interfere na capacidade de frenagem e no funcionamento da suspensão do veículo, causas frequentes de acidentes.
Ciente dessa responsabilidade e com base na experiência adquirida com pesagens, um caminhoneiro sabe que seu caminhão pode carregar, no máximo, 1 500 telhas ou 1 200 tijolos.
Para o reflorestamento de uma área, deve-se cercar - ENEM 2013
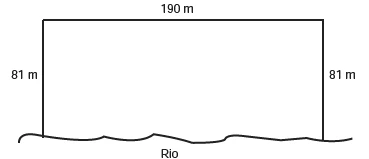
MatemáticaPara o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento.
Para aumentar as vendas no início do ano, uma loja de - ENEM 2013
MatemáticaPara aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.
Foi realizado um levantamento nos 200 hotéis de uma cidade - ENEM 2013
MatemáticaFoi realizado um levantamento nos 200 hotéis de uma cidade, no qual foram anotados os valores, em reais, das diárias para um quarto padrão de casal e a quantidade de hotéis para cada valor da diária. Os valores das diárias foram: A = R$ 200,00; B = R$ 300,00; C = R$ 400,00 e D = R$ 600,00. No gráfico, as áreas representam as quantidades de hotéis pesquisados, em porcentagem, para cada valor da diária.

Deseja-se postar cartas não comerciais, sendo duas de 100 - ENEM 2013
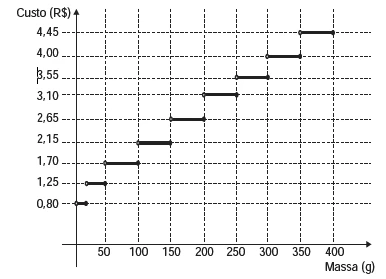
MatemáticaDeseja-se postar cartas não comerciais, sendo duas de 100 g, três de 200 g e uma de 350 g. O gráfico mostra o custo para enviar uma carta não comercial pelos Correios:
Cinco empresas de gêneros alimentícios encontram-se à - ENEM 2013
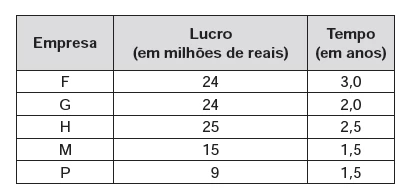
MatemáticaCinco empresas de gêneros alimentícios encontram-se à venda. Um empresário, almejando ampliar os seus investimentos, deseja comprar uma dessas empresas. Para escolher qual delas irá comprar, analisa o lucro (em milhões de reais) de cada uma delas, em função de seus tempos (em anos) de existência, decidindo comprar a empresa que apresente o maior lucro médio anual. O quadro apresenta o lucro (em milhões de reais) acumulado ao longo do tempo (em anos) de existência de cada empresa.
Para se construir um contrapiso, é comum, na constituição - ENEM 2013
MatemáticaPara se construir um contrapiso, é comum, na constituição do concreto, se utilizar cimento, areia e brita, na seguinte proporção: 1 parte de cimento, 4 partes de areia e 2 partes de brita. Para construir o contrapiso de uma garagem, uma construtora encomendou um caminhão betoneira com 14 m³ de concreto.
O contribuinte que vende mais de R$ 20 mil de ações em - ENEM 2013
MatemáticaO contribuinte que vende mais de R$ 20 mil de ações em Bolsa de Valores em um mês deverá pagar Imposto de Renda. O pagamento para a Receita Federal consistirá em 15% do lucro obtido com a venda das ações.
Num parque aquático existe uma piscina infantil na forma - ENEM 2013
MatemáticaNum parque aquático existe uma piscina infantil na forma de um cilindro circular reto, de 1 m de profundidade e volume igual a 12 m³, cuja base tem raio R e centro O. Deseja-se construir uma ilha de lazer seca no interior dessa piscina, também na forma de um cilindro circular reto, cuja base estará no fundo da piscina e com centro da base coincidindo com o centro do fundo da piscina, conforme a figura. O raio da ilha de lazer será r. Deseja-se que após a construção dessa ilha, o espaço destinado à água na piscina tenha um volume de, no mínimo, 4 m³.
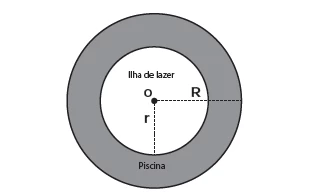
Considere 3 como valor aproximado para π
Uma fábrica de fórmicas produz placas quadradas de lados - ENEM 2013
MatemáticaUma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a uma demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.
Uma indústria tem um reservatório de água com capacidade - ENEM 2013
MatemáticaUma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.
Durante uma aula de Matemática, o professor sugere aos - ENEM 2013
MatemáticaDurante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:
I — é a circunferência de equação x2 + y2 = 9;
II — é a parábola de equação y = − x2 − 1, com x variando de −1 a 1;
III — é o quadrado formado pelos vértices (−2, 1), (−1, 1), (−1, 2) e (−2, 2);
IV — é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
V — é o ponto (0, 0). A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura.
Uma loja acompanhou o número de compradores de dois - ENEM 2013
MatemáticaUma loja acompanhou o número de compradores de dois produtos, A e B, durante os meses de janeiro, fevereiro e março de 2012. Com isso, obteve este gráfico:
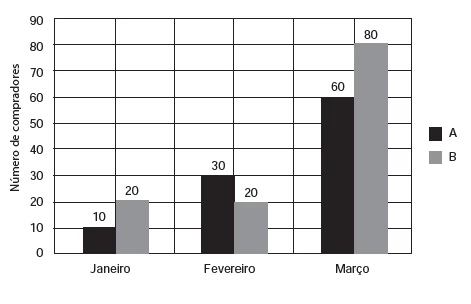
Em um certo teatro, as poltronas são divididas em setores. - ENEM 2013
MatemáticaEm um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas.
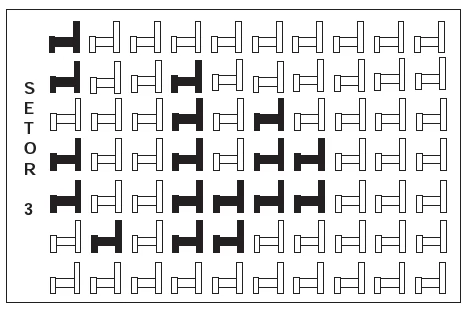
A cidade de Guarulhos (SP) tem o 8º PIB municipal do - ENEM 2013
MatemáticaA cidade de Guarulhos (SP) tem o 8º PIB municipal do Brasil, além do maior aeroporto da América do Sul. Em proporção, possui a economia que mais cresce em indústrias, conforme mostra o gráfico.
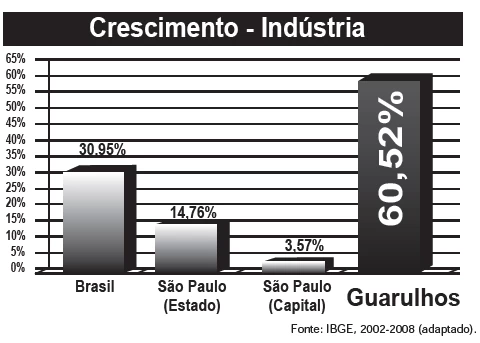
A Lei da Gravitação Universal, de Isaac Newton, estabelece - ENEM 2013
MatemáticaA Lei da Gravitação Universal, de Isaac Newton, estabelece a intensidade da força de atração entre duas massas. Ela é representada pela expressão:
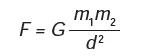
onde m1 e m2 correspondem às massas dos corpos, d à distância entre eles, G à constante universal da gravitação e F à força que um corpo exerce sobre o outro.
O esquema representa as trajetórias circulares de cinco satélites, de mesma massa, orbitando a Terra.
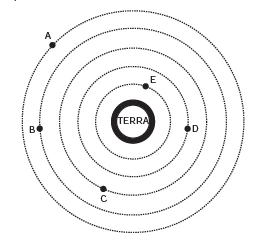
Muitos processos fisiológicos e bioquímicos, tais como - ENEM 2013
MatemáticaMuitos processos fisiológicos e bioquímicos, tais como batimentos cardíacos e taxa de respiração, apresentam escalas construídas a partir da relação entre superfície e massa (ou volume) do animal. Uma dessas escalas, por exemplo, considera que “o cubo da área S da superfície de um mamífero é proporcional ao quadrado de sua massa M”.
A parte interior de uma taça foi gerada pela rotação de - ENEM 2013
MatemáticaA parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
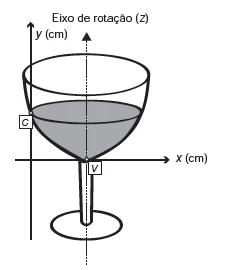
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei f(x) = 3 / 2 x2 – 6x onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
A United Nations human rights official today called on - ENEM 2013
MatemáticaAfter prison blaze kills hundreds in Honduras, UN warns on overcrowding
15 February 2012
A United Nations human rights official today called on Latin American countries to tackle the problem of prison overcrowding in the wake of an overnight fire at a jail in Honduras that killed hundreds of inmates. More than 300 prisoners are reported to have died in the blaze at the prison, located north of the capital, Tegucigalpa, with dozens of others still missing and presumed dead. Antonio Maldonado, human rights adviser for the UN system in Honduras, told UN Radio today that overcrowding may have contributed to the death toll. “But we have to wait until a thorough investigation is conducted so we can reach a precise cause,” he said. “But of course there is a problem of overcrowding in the prison system, not only in this country, but also in many other prisons in Latin America.”
The United Nations Alliance of Civilizations (UNAOC) is - ENEM 2013
MatemáticaDo one thing for diversity and inclusion
The United Nations Alliance of Civilizations (UNAOC) is launching a campaign aimed at engaging people around the world to Do One Thing to support Cultural Diversity and Inclusion. Every one of us can do ONE thing for diversity and inclusion; even one very little thing can become a global action if we all take part in it.
Simple things YOU can do to celebrate the World Day for Cultural Diversity for Dialogue and Development on May 21.
1. Visit an art exhibit or a museum dedicated to other cultures.
2. Read about the great thinkers of other cultures.
3. Visit a place of worship different than yours and participate in the celebration.
4. Spread your own culture around the world and learn about other cultures.
5. Explore music of a different culture.
There are thousands of things that you can do, are you taking part in it?
A partir da leitura dessa tirinha, infere-se que o - ENEM 2013
Matemática
A Secretaria de Saúde de um município avalia um programa - ENEM 2013
MatemáticaA Secretaria de Saúde de um município avalia um programa que disponibiliza, para cada aluno de uma escola municipal, uma bicicleta, que deve ser usada no trajeto de ida e volta, entre sua casa e a escola. Na fase de implantação do programa, o aluno que morava mais distante da escola realizou sempre o mesmo trajeto, representado na figura, na escala 1 : 25 000, por um período de cinco dias.
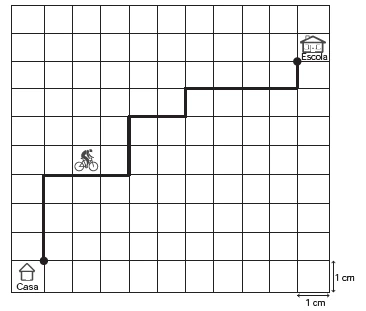
O índice de eficiência utilizado por um produtor de leite - ENEM 2013
MatemáticaO índice de eficiência utilizado por um produtor de leite para qualificar suas vacas é dado pelo produto do tempo de lactação (em dias) pela produção média diária de leite (em kg), dividido pelo intervalo entre partos (em meses). Para esse produtor, a vaca é qualificada como eficiente quando esse índice é, no mínimo, 281 quilogramas por mês, mantendo sempre as mesmas condições de manejo (alimentação, vacinação e outros). Na comparação de duas ou mais vacas, a mais eficiente é a que tem maior índice.
A tabela apresenta os dados coletados de cinco vacas:

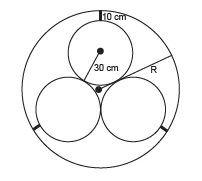
Em um sistema de dutos, três canos iguais, de raio externo - ENEM 2013
MatemáticaEm um sistema de dutos, três canos iguais, de raio externo 30 cm, são soldados entre si e colocados dentro de um cano de raio maior, de medida R. Para posteriormente ter fácil manutenção, é necessário haver uma distância de 10 cm entre os canos soldados e o cano de raio maior. Essa distância é garantida por um espaçador de metal, conforme a figura:
Um comerciante visita um centro de vendas para fazer - ENEM 2013
MatemáticaUm comerciante visita um centro de vendas para fazer cotação de preços dos produtos que deseja comprar. Verifica que se aproveita 100% da quantidade adquirida de produtos do tipo A, mas apenas 90% de produtos do tipo B. Esse comerciante deseja comprar uma quantidade de produtos, obtendo o menor custo/benefício em cada um deles. O quadro mostra o preço por quilograma, em reais, de cada produto comercializado.

Considere o seguinte jogo de apostas: Numa cartela com 60 - ENEM 2013
MatemáticaConsidere o seguinte jogo de apostas:
Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados apenas 6. O apostador será premiado caso os 6 números sorteados estejam entre os números escolhidos por ele numa mesma cartela.
O quadro apresenta o preço de cada cartela, de acordo com a quantidade de números escolhidos.
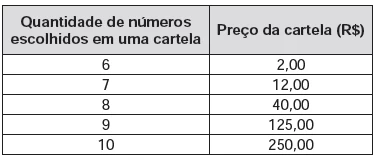
Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:
Arthur: 250 cartelas com 6 números escolhidos;
Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos;
Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos;
Douglas: 4 cartelas com 9 números escolhidos;
Eduardo: 2 cartelas com 10 números escolhidos.
Uma fábrica de parafusos possui duas máquinas, I e II, - ENEM 2013
MatemáticaUma fábrica de parafusos possui duas máquinas, I e II, para a produção de certo tipo de parafuso.
Em setembro, a máquina I produziu 54/100 do total de parafusos produzidos pela fábrica. Dos parafusos produzidos por essa máquina, 25/1 000 eram defeituosos. Por sua vez, 38/1 000 dos parafusos produzidos no mesmo mês pela máquina II eram defeituosos.
O desempenho conjunto das duas máquinas é classificado conforme o quadro, em que P indica a probabilidade de um parafuso escolhido ao acaso ser defeituoso.

A cerâmica constitui-se em um artefato bastante presente - ENEM 2013
MatemáticaA cerâmica constitui-se em um artefato bastante presente na história da humanidade. Uma de suas várias propriedades é a retração (contração), que consiste na evaporação da água existente em um conjunto ou bloco cerâmico quando submetido a uma determinada temperatura elevada. Essa elevação de temperatura, que ocorre durante o processo de cozimento, causa uma redução de até 20% nas dimensões lineares de uma peça.
Gangorra é um brinquedo que consiste de uma tábua longa e - ENEM 2013
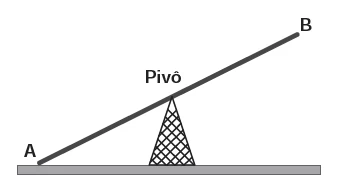
MatemáticaGangorra é um brinquedo que consiste de uma tábua longa e estreita equilibrada e fixada no seu ponto central (pivô). Nesse brinquedo, duas pessoas sentam-se nas extremidades e, alternadamente, impulsionam-se para cima, fazendo descer a extremidade oposta, realizando, assim, o movimento da gangorra.
Considere a gangorra representada na figura, em que os pontos A e B são equidistantes do pivô:
O dono de um sítio pretende colocar uma hastede - ENEM 2013
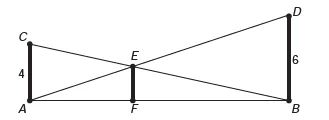
MatemáticaO dono de um sítio pretende colocar uma hastede sustentação para melhor firmar dois postes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.
Um restaurante utiliza, para servir bebidas, bandejas com - ENEM 2013
MatemáticaUm restaurante utiliza, para servir bebidas, bandejas com bases quadradas. Todos os copos desse restaurante têm o formato representado na figura:
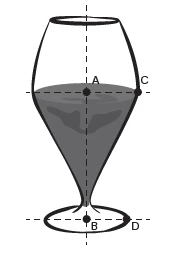
O cruzamento da quantidade de horas estudadas como - ENEM 2013
MatemáticaUma falsa relação
O cruzamento da quantidade de horas estudadas como desempenho no Programa Internacional de Avaliação de Estudantes (Pisa) mostra que mais tempo na escola não é garantia de nota acima da média.
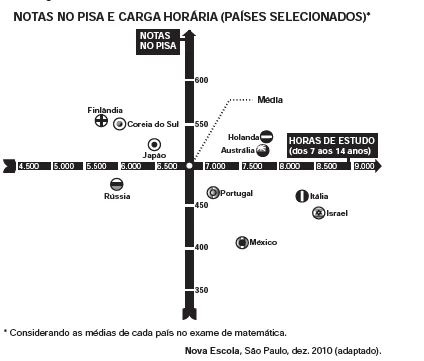
Uma cozinheira, especialista em fazer bolos, utiliza uma - ENEM 2013
MatemáticaUma cozinheira, especialista em fazer bolos, utiliza uma forma no formato representado na figura:
Nela identifica-se a representação de duas figuras geométricas tridimensionais.
Nos últimos anos, a televisão tem passado por uma - ENEM 2013
MatemáticaNos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
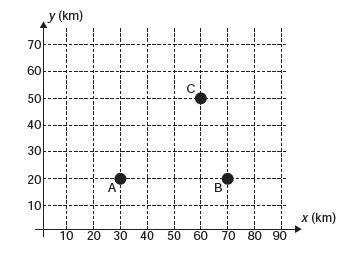
A torre deve estar situada em um local equidistante das três antenas.
A figura apresenta dois mapas, em que o estado do Rio de - ENEM 2013
MatemáticaA figura apresenta dois mapas, em que o estado do Rio de Janeiro é visto em diferentes escalas.
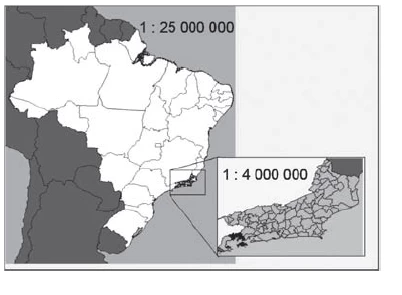
Há interesse em estimar o número de vezes que foi ampliada a área correspondente a esse estado no mapa do Brasil.
O ciclo de atividade magnética do Sol tem um período de - ENEM 2013
MatemáticaO ciclo de atividade magnética do Sol tem um período de 11 anos. O início do primeiro ciclo registrado se deu no começo de 1755 e se estendeu até o final de 1765. Desde então, todos os ciclos de atividade magnética do Sol têm sido registrados.
A projeção ortogonal sobre o plano do solo do trajeto - ENEM 2021
MatemáticaO Atomium, representado na imagem, é um dos principais pontos turísticos de Bruxelas. Ele foi construído em 1958 para a primeira grande exposição mundial depois da Segunda Guerra Mundial, a Feira Mundial de Bruxelas. Trata-se de uma estrutura metálica construída no formato de um cubo. Essa estrutura está apoiada por um dos vértices sobre uma base paralela ao plano do solo e a diagonal do cubo, contendo esse vértice, é ortogonal ao plano da base. Centradas nos vértices desse cubo, foram construídas oito esferas metálicas, e uma outra esfera foi construída centrada no ponto de interseção das diagonais do cubo. As oito esferas sobre os vértices são interligadas segundo suas arestas, e a esfera central se conecta a elas pelas diagonais do cubo. Todas essas interligações são feitas por tubos cilíndricos que possuem escadas em seu interior, permitindo o deslocamento de pessoas pela parte interna da estrutura. Na diagonal ortogonal à base, o deslocamento é feito por um elevador, que permite o deslocamento entre as esferas da base e a esfera do ponto mais alto, passando pela esfera central. Considere um visitante que se deslocou pelo interior do Atomium sempre em linha reta e seguindo o menor trajeto entre dois vértices, passando por todas as arestas e todas as diagonais do cubo.

Um segmento de reta está dividido em duas partes na - ENEM 2021
MatemáticaUm segmento de reta está dividido em duas partes na proporção áurea quando o todo está para uma das partes na mesma razão em que essa parte está para a outra. Essa constante de proporcionalidade é comumente representada pela letra grega ϕ, e seu valor é dado pela solução positiva da equação ϕ² = ϕ + 1.
Assim como a potência ϕ², as potências superiores de w podem ser expressas da forma aϕ + b, em que a e b são inteiros positivos, como apresentado no quadro.
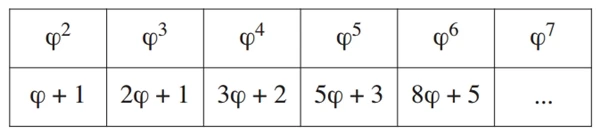
Qual expressão determina a quantidade de painéis diferentes que - ENEM
MatemáticaA Copa do Brasil teve, até a edição de 2018, 15 times diferentes como campeões da competição, conforme apresentado na imagem. Suponha que, como homenagem aos times campeões, a Confederação Brasileira de Futebol a cada edição da competição, com o nome do time vencedor, o brasão e o ano do título. O painel deve se fabricado de modo que a primeira linha só tenha clubes gaúchos (Internacional, Grêmio e Juventude); a segunda, apenas times cariocas (Flamengo, Vasco e Fluminense); a terceira, somente times mineiros (Cruzeiro e Atlético Mineiro); a quarta, exclusivamente clubes paulistas (Corinthians, Palmeiras, Santos, Paulista FC, Santo André), e as duas últimas sem nenhuma restrição.

O organizador de uma competição de lançamento de dardos - ENEM 2021
MatemáticaO organizador de uma competição de lançamento de dardos pretende tornar o campeonato mais competitivo. Pelas regras atuais da competição, numa rodada, o jogador lança 3 dardos e pontua caso acerte pelo menos um deles no alvo. O organizador considera que, em média, os jogadores têm, em cada lançamento, 1/2 de probabilidade de acertar um dardo no alvo.
A fim de tornar o jogo mais atrativo, planeja modificar as regras de modo que a probabilidade de um jogador pontuar em uma rodada seja igual ou superior a 9/10. Para isso, decide aumentar a quantidade de dardos a serem lançados em cada rodada.
Aplicativos que gerenciam serviços de hospedagem têm - ENEM 2021
MatemáticaAplicativos que gerenciam serviços de hospedagem têm ganhado espaço no Brasil e no mundo por oferecer opções diferenciadas em termos de localização e valores de hospedagem. Em um desses aplicativos, o preço P a ser pago pela hospedagem é calculado considerando um preço por diária d, acrescido de uma taxa fixa de limpeza L e uma taxa de serviço. Essa taxa de serviço é um valor percentual s calculado sobre o valor pago pelo total das diárias.
Uma grande rede de supermercados adota um sistema de - ENEM 2021
MatemáticaUma grande rede de supermercados adota um sistema de avaliação dos faturamentos de suas filiais, considerando a média de faturamento mensal em milhão. A matriz da rede paga uma comissão para os representantes dos supermercados que atingirem uma média de faturamento mensal (M), conforme apresentado no quadro.
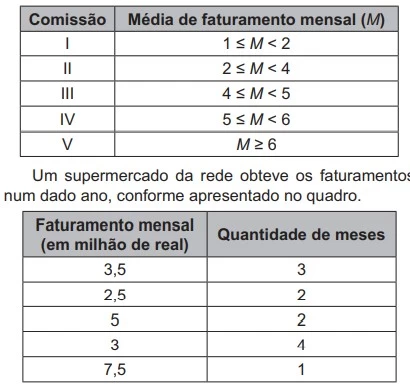
Com base nessas informações, a gerência decidiu incluir no - ENEM 2021
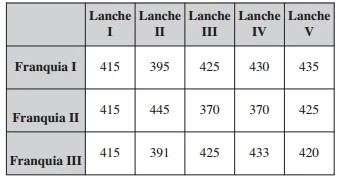
MatemáticaUma rede de hamburgueria tem três franquias em cidades distintas. Visando incluir um novo tipo de lanche no cardápio, o gerente de marketing da rede sugeriu que fossem colocados à venda cinco novos tipos de lanche, em edições especiais. Os lanches foram oferecidos pelo mesmo período de tempo em todos os franqueados. O tipo que apresentasse a maior média por franquia seria incluído definitivamente no cardápio. Terminado o período de experiência, a gerência recebeu um relatório descrevendo as quantidades vendidas, em unidade, de cada um dos cinco tipos de lanche nas três franquias.
A substituição da ração ocorrerá se a média da distribuição- ENEM 2021
MatemáticaUm zootecnista pretende testar se uma nova ração para coelhos é mais eficiente do que a que ele vem utilizando atualmente. A ração atual proporciona uma massa média de 10 kg por coelho, com um desvio padrão de 1 kg, alimentado com essa ração durante um período de três meses.
O zootecnista selecionou uma amostra de coelhos e os alimentou com a nova ração pelo mesmo período de tempo. Ao final, anotou a massa de cada coelho, obtendo um desvio padrão de 1,5 kg para a distribuição das massas dos coelhos dessa amostra. Para avaliar a eficiência dessa ração, ele utilizará o coeficiente de variação (CV) que é uma medida de dispersão definida por CV =S/X, em que s representa o desvio padrão X, a média das massas dos coelhos que foram alimentados com uma determinada ração.
O zootecnista substituirá a ração que vinha utilizando pela nova, caso o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a nova ração for menor do que o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a ração atual.
Em um estudo realizado pelo IBGE em quatro estados e no - ENEM 2021
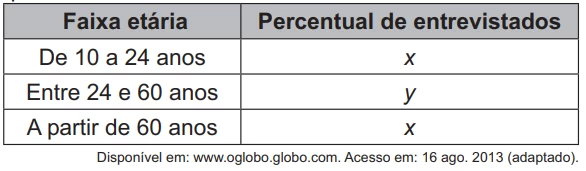
MatemáticaEm um estudo realizado pelo IBGE em quatro estados e no Distrito Federal, com mais de 5 mil pessoas com 10 anos ou mais, observou-se que a leitura ocupa, em média, apenas seis minutos do dia de cada pessoa. Na faixa de idade de 10 a 24 anos, a média diária é de três minutos. No entanto, no grupo de idades entre 24 e 60 anos, o tempo médio diário dedicado à leitura é de 5 minutos. Entre os mais velhos, com 60 anos ou mais, a média é de 12 minutos.
A quantidade de pessoas entrevistadas de cada faixa de idade seguiu a distribuição percentual descrita no quadro.
Uma pessoa realizou uma pesquisa com alguns alunos de uma - ENEM 2021
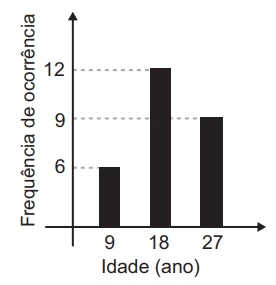
MatemáticaUma pessoa realizou uma pesquisa com alguns alunos de uma escola, coletando suas idades, e organizou esses dados no gráfico.
O gráfico apresenta o nível de ocupação dos cinco - ENEM 2021
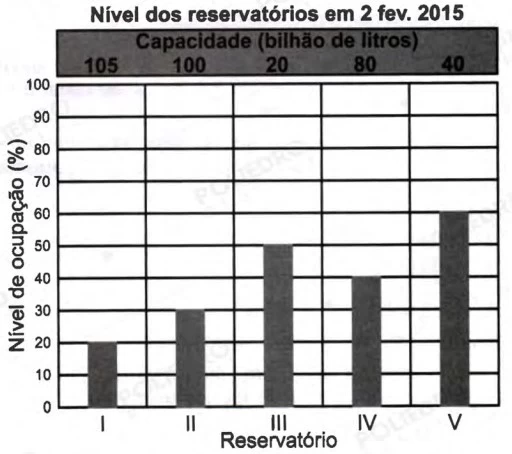
MatemáticaO gráfico apresenta o nível de ocupação dos cinco reservatórios de água que abasteciam uma cidade em 2 de Fevereiro de 2015.
Um pesquisador acredita que a mediana representa bem o - ENEM 2021
MatemáticaO quadro apresenta o número de terremotos de magnitude maior ou igual a 7, na escala de Richter, ocorridos em nosso planeta nos anos 2000 e 2011.

Após codificar esse texto com a regra do exemplo fornecido - ENEM 2021
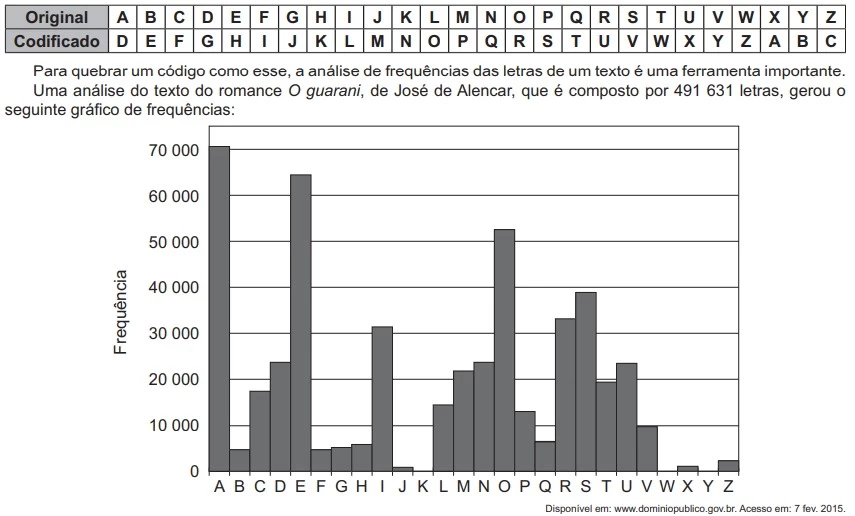
MatemáticaA cifra de César é um exemplo de um método de codificação de mensagens usado por Júlio César para se comunicar com seus generais.
No método, cada letra era trocada por uma letra que aparência no alfabeto por um número fixo de casas adiante (ou atrás) de forma cíclica. A seguir temos um exemplo em que casa letra é substituída pela que vem três posições à frente.
Com base no gráfico obtido, o menor preço, p (em mil reais)- ENEM 2021
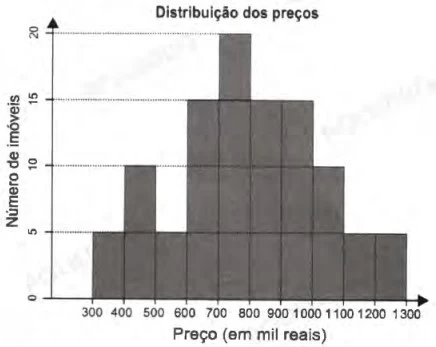
MatemáticaUm casal está planejando comprar um apartamento de dois quartos num bairro de uma cidade e consultou a página de uma corretora de imóveis, encontrando 105 apartamentos de dois quartos à venda no bairro desejado. Eles usaram um aplicativo da corretora para gerar a distribuição dos preços do conjunto de imóveis selecionados.
O gráfico ilustra a distribuição de frequências dos preços de venda dos apartamentos dessa lista (em mil reais), no qual as faixas de preço são dadas por [300, 400], [400, 500], [500, 600], [600, 700], [700, 800], [800, 900], [900, 1 000], [1 000, 1 100], [1 100, 1 200] e [1 200, 1 300].
A mesma corretora anuncia que cerca de 50% dos apartamentos de dois quartos nesse bairro, publicados em sua página, têm preço de venda inferior a 550 mil reais. No entanto, o casal achou que essa última informação não era compatível com o gráfico obtido.
A depressão caracteriza-se por um desequilíbrio na química - ENEM 2021
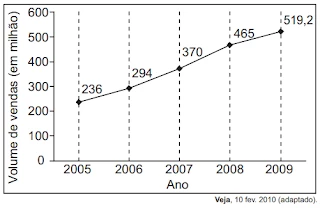
MatemáticaA depressão caracteriza-se por um desequilíbrio na química cerebral. Os neurônios de um deprimido não respondem bem as estímulos dos neurotransmissores.
Os remédios que combatem a depressão têm o objetivo de restabelecer a química cerebral. Com o aumento gradativo de casos de depressão, a venda desses medicamentos está em crescente evolução, conforme ilustra o gráfico.
Nessas condições, o lucro mensal para os próximos meses - ENEM 2021
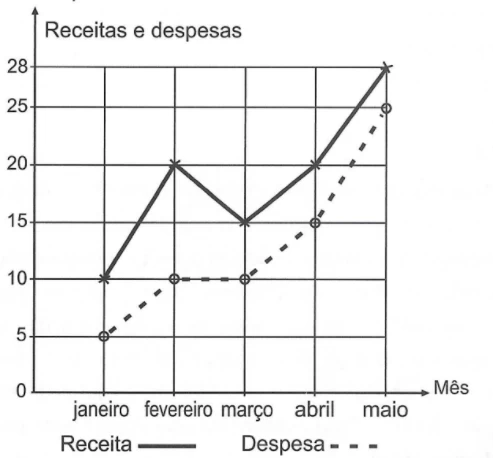
MatemáticaA receita R de uma empresa ao final de um mês é o dinheiro captado com a venda de mercadorias ou com a prestação de serviços nesse mês, e a despesa D é todo o dinheiro utilizado para pagamento de salários, contas de água e luz, impostos, entre outros. O lucro mensal obtido ao final do mês é a diferença entre a receita e a despesa registradas no mês. O gráfico apresenta as receitas e despesas, em milhão de real, de uma empresa ao final dos cinco primeiros meses de um dado ano.
O número, com duas casas na parte decimal, mais próximo do - ENEM 2021
MatemáticaA demografia médica é o estudo da população de médicos no Brasil nos aspectos quantitativo e qualitativo, sendo um dos seus objetivos fazer projeções sobre a necessidade da formação de novos médicos. Um desses estudos gerou um conjunto de dados que aborda a evolução do número de médicos e da população brasileira por várias décadas. O quadro apresenta parte desses dados.
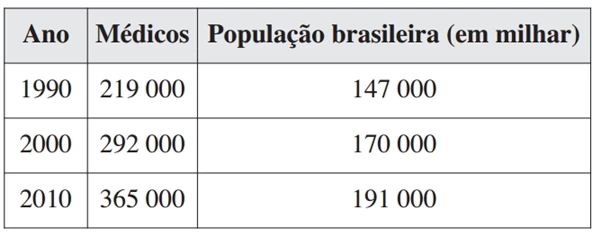
Segundo uma projeção estatística, a variação do número de médicos e o da população brasileira de 2010 para 2020 será a média entre a variação de 1990 para 2000 e a de 2000 para 2010. Com o resultado dessa projeção, determina-se o número de médicos por mil habitantes no ano de 2020.
Um parque temático brasileiro construiu uma réplica em - ENEM 2021
MatemáticaUm parque temático brasileiro construiu uma réplica em miniatura do castelo de Liechtenstein. O castelo original, representado na imagem, está situado na Alemanha e foi reconstruído entre os anos de 1840 e 1842, após duas destruições causadas por guerras.

O castelo possui uma ponte de 38,4m de comprimento e 1,68m de largura. O artesão que trabalhou para o parque produziu a réplica do castelo, em escala. Nessa obra, as medidas do comprimento e da largura da ponte eram, respectivamente, 160cm e 7 cm.
Para a comunicação entre dois navios é utilizado um sistema- ENEM 2021
MatemáticaPara a comunicação entre dois navios é utilizado um sistema de codificação com base em valores numéricos. Para isso, são consideradas as operações triângulo Δ e estrela , definidas sobre o conjunto dos números reais por xΔy = x² + xy – y² e x * y = xy + x.
O navio que deseja enviar uma mensagem deve fornecer um valor de entrada b, que irá gerar um valor de saída, a ser enviado ao navio receptor, dado pela soma das duas maiores soluções da equação (aΔb)*(bΔa) = 0 . Cada valor possível de entrada e saída representa uma mensagem diferente já conhecida pelos dois navios.
Um navio deseja enviar ao outro a mensagem “ATENÇÃO!”. Para isso, deve utilizar o valor de entrada b=1.
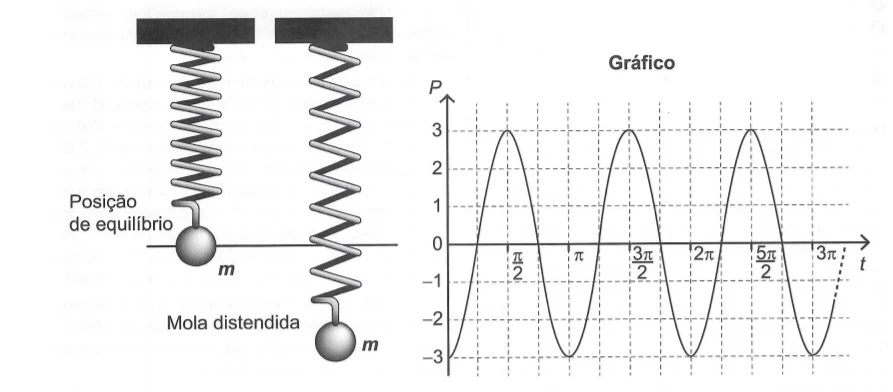
A expressão algébrica que representa as posições P(t) da - ENEM 2021
MatemáticaUma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) =± A cos(ωt) ou P(t) =± A sen(ωt), em que A > 0 é a amplitude do deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula ω = 2π/T.
Considera a ausência de quaisquer forças dissipativas.
Qual deve ser a redução percentual da quantidade de frango - ENEM 2021
MatemáticaUm atleta produz sua própria refeição com custo fixo de R$ 10,00. Ela é composta por 400g de frango, 600g de batata-doce e uma hortaliça. Atualmente, os preços dos produtos para essa refeição são:

Em relação a esses preços, haverá um aumento de 50% no preço do quilograma de batata-doce, e os outros preços não serão alterados. O atleta deseja manter o custo da refeição, a quantidade de batata-doce e a hortaliça. Portanto, terá que reduzir a quantidade de frango.
Um nutricionista verificou, na dieta diária do seu cliente - ENEM 2021
MatemáticaUm nutricionista verificou, na dieta diária do seu cliente, a falta de 800mg do mineral A, de 1 000 mg do mineral B e de 1 200 mg do mineral C. Por isso, recomendou a compra de suplementos alimentares que forneçam os minerais faltantes e informou que não haveria problema se consumisse mais desses minerais do que o recomendado.
O cliente encontrou cinco suplementos, vendidos em sachês unitários, cujos preços e as quantidades dos minerais estão apresentados a seguir:
Suplemento I: contém 50mg do mineral A, 100mg do mineral B e 200 mg do mineral C e custa R$2,00;
Suplemento II: contém 800mg do mineral A, 250mg do mineral B e 200 mg do mineral C e custa R$3,00;
Suplemento III: contém 250mg do mineral A, 1 000mg do mineral B e 300 mg do mineral C e custa R$5,00;
Suplemento IV: contém 600mg do mineral A, 500mg do mineral B e 1 000 mg do mineral C e custa R$6,00;
Suplemento V: contém 400mg do mineral A, 800mg do mineral B e 1 200 mg do mineral C e custa R$8,00;
O cliente decidiu comprar sachês de um único suplemento no qual gastasse menos dinheiro e ainda suprisse a falta de minerais indicada pelo nutricionista, mesmo que consumisse alguns deles além de sua necessidade.
Nessa parada específica, com um dos grupos reduzido, qual - ENEM 2021
MatemáticaEm uma corrida automobilística, os carros podem fazer paradas nos boxes para efetuar trocar de pneus. Nessas trocas, o trabalho é feito por um grupo de três pessoas em cada pneu. Considere que os grupos iniciam o trabalho no mesmo instante, trabalham à mesma velocidade e cada grupo trabalha em um único pneu. Com os quatro grupos completos, são necessários 4 segundos para que a troca seja efetuada. O tempo gasto por um grupo para trocar um pneu é inversamente proporcional ao número de pessoas trabalhando nele. Em uma dessas paradas, um dos trabalhadores passou mal, não pôde participar da troca e nem foi substituído, de forma que um dos quatro grupos de troca ficou reduzido.
A quantidade de combustível consumida pelo modelo de - ENEM 2021
MatemáticaPara realizar um voo entre duas cidades que distam 2 000 km uma da outra, uma companhia aérea utilizava um modelo de aeronave A, capaz de transportar até 200 passageiros. Quando uma dessas aeronaves está lotada de passageiros, o consumo de combustível é de 0,02 litro por quilômetro e por passageiro. Essa companhia resolveu trocar o modelo de aeronave A pelo modelo de aeronave B, que é capaz de transportar 10% de passageiros a mais do que o modelo A, mas consumindo 10% menos combustível por quilômetro e por passageiro.
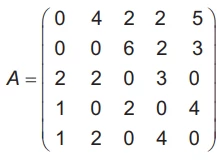
Uma construtora, pretendendo investir na construção de - ENEM 2021
MatemáticaUma construtora, pretendendo investir na construção de imóveis em uma metrópole com cinco grandes regiões, fez uma pesquisa sobre a quantidade de famílias que mudaram de uma região para outra, de modo a determinar qual região foi o destino do maior fluxo de famílias, sem levar em consideração o número de famílias que deixaram a região. Os valores da pesquisa estão dispostos em uma matriz A = [aij], i,j ∈ {1,2,3,4,5}, em que o elemento aij corresponde ao total de famílias (em dezena) que se mudaram da região i para a região j durante um certo período, e o elemento aii é considerado nulo, uma vez que somente são consideradas mudanças entre regiões distintas. A seguir, está apresentada a matriz com os dados da pesquisa.
O gráfico que mais se assemelha ao que deve ser elaborado - ENEM 2021
MatemáticaO administrador de um teatro percebeu que, com o ingresso do evento a R$20,00, um show conseguia atrair 200 pessoas e que, a cada R$1,00 de redução no preço do ingresso, o número de pessoas aumentava em 40. Ele sabe que os donos do teatro só admitem trabalhar com valores inteiros para os ingressos, pela dificuldade de disponibilizar troco, e pretende convencê-los a diminuir o preço do ingresso. Assim, apresentará um gráfico da arrecadação em função do valor do desconto no preço atual do ingresso.
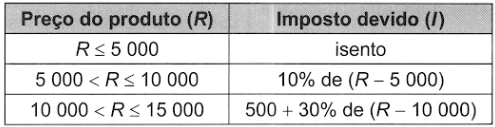
O quadro representa a relação entre o preço de um produto - ENEM 2021
MatemáticaO quadro representa a relação entre o preço de um produto (R) e seu respectivo imposto devido (l).
Nas condições apresentadas, o reservatório deverá ser - ENEM 2021
MatemáticaUm povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.
Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π.
Qual dos fornecedores prestou as informações adequadas - ENEM 2021
MatemáticaO projeto de um contêiner, em forma de paralelepípedo reto retangular, previa a pintura dos dois lados (interno e externo) de cada uma das quatro paredes com tinta acrílica e a pintura do piso interno com tinta epóxi. O construtor havia pedido, a cinco fornecedores diferentes, orçamentos das tintas necessárias, mas, antes de iniciar a obra, resolveu mudar o projeto original, alterando o comprimento e a largura para o dobro do originalmente previsto, mantendo inalterada a altura. Ao pedir novos orçamentos aos fornecedores, para as novas dimensões, cada um deu uma resposta diferente sobre as novas quantidades de tinta necessárias.
Em relação ao previsto para o projeto original, as novas quantidades de tinta necessárias informadas pelos fornecedores foram as seguintes:
– Fornecedor I: “O dobro, tanto para as paredes quanto para o piso”.
– Fornecedor II: “O dobro para as paredes e quatro vezes para o piso”.
– Fornecedor III: “Quatro vezes, tanto para as paredes quanto para o piso”.
– Fornecedor IV: “Quatro vezes para as paredes e o dobro para o piso”.
– Fornecedor V: “Oito vezes para as paredes e quatro vezes para o piso”.
Analisando as informações dos fornecedores, o construtor providenciará a quantidade adequada de material. Considere a porta de acesso do contêiner como parte de uma das paredes.
O valor do desempenho médio do automóvel com o novo motor - ENEM 2021
MatemáticaUm automóvel apresenta um desempenho médio de 16 km/L. Um engenheiro desenvolveu um novo motor a combustão que economiza, em relação ao consumo do motor anterior, 0,1 L de combustível a cada 10 km percorridos.
Qual a quantidade máxima de camisetas que essa pessoa - ENEM 2021
MatemáticaUma pessoa pretende viajar por uma companhia aérea que despacha gratuitamente uma mala com até 10kg.
Em duas viagens que realizou, essa pessoa utilizou a mesma mala e conseguiu 10 kg com as seguintes combinações de itens:
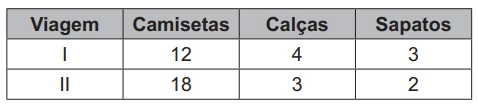
Para ter certeza de que sua bagagem terá massa de 10 kg, ela decide levar essa mala com duas calças, um sapato e o máximo de camisetas, admitindo que itens do mesmo tipo têm a mesma massa.
Nessa relação, a unidade de medida adequada para o módulo - ENEM 2021
MatemáticaA relação de Newton-Laplace estabelece que o módulo volumétrico de um fluído é diretamente proporcional ao quadrado da velocidade do som (em metro por segundo) no fluido e à sua densidade (em quilograma por meto cúbico), com uma constante de proporcionalidade adimensional.
Nessas condições, o modelo que deverá ser escolhido tem com- ENEM 2021
MatemáticaO dono de uma loja pretende usar cartões imantados para a sua divulgação de sua loja. A empresa que fornecerá o serviço lhe informa que o custo de fabricação do cartão é de R$0,01 por centímetro quadrado e que disponibiliza modelos tendo como faces úteis para impressão:
* um triângulo equilátero de lado 12 cm;
* um quadrado de lado 8 cm;
* um retângulo de lados 11 cm e 8 cm;
* um hexágono regular de lado 6cm;
* um círculo de diâmetro 10 cm.
O dono da loja está disposto a pagar, no máximo, R$0,80 por cartão. Ele escolherá, dentro desse limite de preço, o modelo que tiver maior área de impressão.
Use 3 como aproximação para π e use 1,7 como aproximação para √3.
Qual é a capacidade volumétrica, em milímetro, dessa caneca- ENEM 2021
MatemáticaUma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
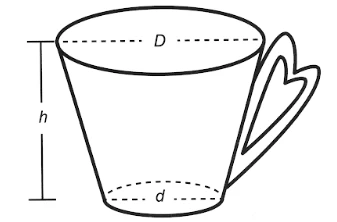
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Nessas condições, o valor que mais se aproxima da medida do- ENEM 2021
MatemáticaO instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.
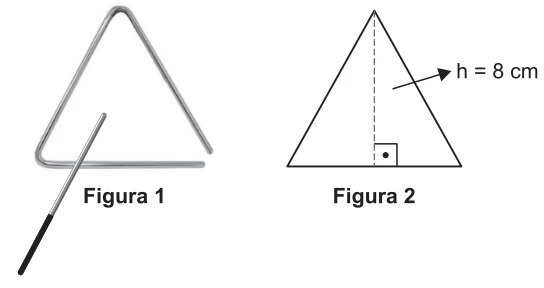
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2.
Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura, Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual ao perímetro do triângulo equilátero representado na Figura 2.
Considere 1,7 como valor aproximado para √3.
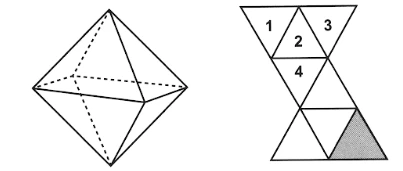
Qual(is) face(s) ficará(ão) oposta(s) à face de cor cinza - ENEM 2021
MatemáticaNum octaedro regular, duas faces são consideradas opostas quando não têm nem arestas, nem vértices em comum. Na figura, observa-se um octaedro regular e uma de suas planificações, na qual há uma face colorida na cor cinza escuro e outras quatro faces numeradas.
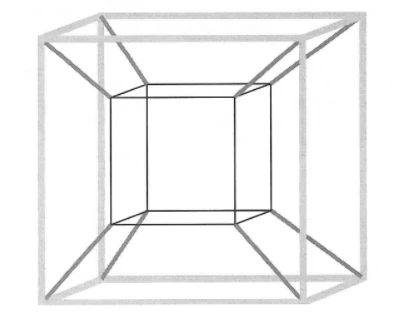
Com base na proposta apresentada, quantas figuras geométricas - ENEM
MatemáticaMuitos brinquedos que frequentemente são encontrados em praças e parques públicos apresentam formatos de figuras geométricas bidimensionais e tridimensionais. Uma empresa foi contratada para desenvolver uma nova forma de brinquedo. A proposta apresentada pela empresa foi de uma estrutura formada apenas por hastes metálicas, conectadas umas às outras, como apresentado na figura. As hastes de mesma tonalidade e espessura são congruentes.
De acordo com as informações fornecidas, o paciente deve - ENEM 2021
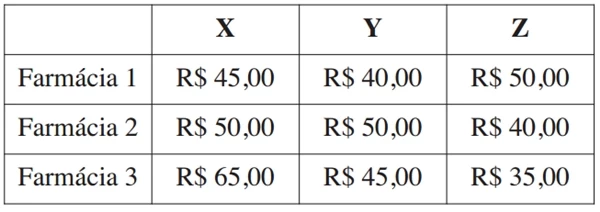
MatemáticaApós a consulta médica, um paciente deve seguir um tratamento composto por três medicamentos: X, Y e Z. O paciente, para adquirir os três medicamentos, faz um orçamento em três farmácias diferentes, conforme o quadro.
Dessas farmácias, algumas oferecem descontos:
na compra dos medicamentos X e Y na Farmácia 2, recebe-se um desconto de 20% em ambos os produtos, independentemente da compra do medicamento Z, e não há desconto para o medicamento Z;
na compra dos 3 medicamentos na Farmácia 3, recebe-se 20% de desconto no valor total da compra. O paciente deseja efetuar a compra de modo a minimizar duas despesa com os medicamentos.
Para não ter prejuízo, o menor número de lavagens diárias - ENEM 2021
MatemáticaUm lava-rápido oferece dois tipos de lavagem de veículos: lavagem simples, ao preço de R$ 20,00, e lavagem completa, ao preço de R$35,00. Para cobrir as despesas com produtos e funcionários, e não ter prejuízos, o lava-rápido deve ter uma receita diária de, pelo menos, R$300,00.
Os trechos do percurso nos quais esse ciclista se mantém - ENEM 2021
MatemáticaUm ciclista amador de 61 anos de idade utilizou um monitor cardíaco para medir suas frequências cardíacas em quatro diferentes tipos de trechos do percurso. Os resultados das frequências cardíacas máximas alcançadas nesses trechos foram:
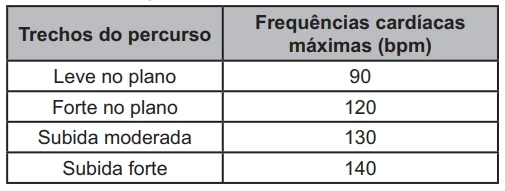
Sabe-se que a faixa aeróbica ideal para o ganho de condicionamento físico é entre 65% e 85% da frequência cardíaca máxima (Fc máx), que, por sua vez, é determinada pela fórmula:
Fc máx. = 220 – idades,
em que a idade é dada em ano e Fc máx. é dada em bpm (batimento por minuto).
A economia da escola, na utilização de um laboratório tipo - ENEM 2021
MatemáticaOs diretores de uma escola precisam construir um laboratório para uso dos alunos. Há duas possibilidades:
(i) um laboratório do tipo A, com capacidade para 100 usuários, a um custo de 180 mil reais e gastos de 60 mil reais por ano para manutenção;
(ii) um laboratório do tipo B, com capacidade para 80 usuários, a um custo de 120 mil reais e gastos com manutenção de 16 mil reais por ano.
Considera-se que, em qualquer caso, o laboratório implantado será utilizado na totalidade de sua capacidade.
A quantidade de fantasias com materiais diferentes que pode- ENEM 2021
MatemáticaUma pessoa produzirá uma fantasia utilizando como materiais: 2 tipos de tecidos diferentes e 5 tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição 6 tecidos diferentes e 15 pedras ornamentais distintas.
Nas condições estabelecidas, o valor total, em real, obtido- ENEM 2021
MatemáticaUma unidade de medida comum usada para expressar áreas de terrenos de grandes dimensões é o hectare, que equivale a 10.000 m². Um fazendeira decide fazer um loteamento utilizando 3 hectares de sua fazenda, dos quais 0,9 hectare será usado para a construção de ruas e calçadas e o restante será dividido em terrenos com área de 300 m² cada um. Os 20 primeiros terrenos vendidos terão preços promocionais de R$ 20.000,00 cada, e os demais, R$30.000,00 cada.
Considerando as informações as informações do texto - ENEM 2021
MatemáticaUma das bases mais utilizadas para representar um número é a base decimal. Entretanto, os computadores trabalham com números na base binária. Nessa base, qualquer número natural é representado usando apenas os algarismos 0 e 1. Por exemplo, as representações dos números 9 e 12, na base binária, são 1001 e 1100, respectivamente. A operação de adição, na base decimal, como detalhado no quadro:

Quantos anos de fundação essa cidade comemorará em 2050? - ENEM 2021
MatemáticaO sistema de numeração romano ainda é utilizado na indicação de capítulos e volumes de livros, na designação de séculos e, em ordem cronológica, de papas e reis de mesmo nome. São utilizadas sete letras do alfabeto:
Quatro fundamentais: I (vale 1); X (vale 10); C (vale 100) e M (vale 1 000).
Três secundárias: V (vale 5); L (vale 50); e D (vale 500).
As regras para escrever números romanos são:
1. Não existe símbolo correspondente ao zero;
2. Os símbolos fundamentais podem ser repetidos até três vezes e seus valores são adicionados. Exemplo: XXX = 30;
3. Uma letra posta à esquerda de outra de maior valor indica subtração dos respectivos valores. Exemplo: IX = 10 – 1 = 9;
4. Uma letra posta à direita de outra de maior valor indica adição dos respectivos valores. Exemplo: XI = 10 + 1 = 11
Em uma cidade europeia há uma placa indicando o ano de sua fundação: MCDLXIX.
Os vidros para veículos produzidos por certo fabricante - ENEM 2014
MatemáticaOs vidros para veículos produzidos por certo fabricante têm transparências entre 70% e 90%, dependendo do lote fabricado. Isso significa que, quando um feixe luminoso incide no vidro, uma parte entre 70% e 90% da luz consegue atravessá-lo. Os veículos equipados com vidros desse fabricante terão instaladas, nos vidros das portas, películas protetoras cuja transparência, dependendo do lote fabricado, estará entre 50% e 70%. Considere que uma porcentagem P da intensidade da luz, proveniente de uma fonte externa, atravessa o vidro e a película.
Durante uma epidemia de uma gripe viral, o secretário de - ENEM 2014
MatemáticaDurante uma epidemia de uma gripe viral, o secretário de saúde de um município comprou 16 galões de álcool em gel, com 4 litros de capacidade cada um, para distribuir igualmente em recipientes para 10 escolas públicas do município. O fornecedor dispõe à venda diversos tipos de recipientes, com suas respectivas capacidades listadas:
Recipiente I: 0,125 litro
Recipiente II: 0,250 litro
Recipiente III: 0,320 litro
Recipiente IV: 0,500 litro
Recipiente V: 0,800 litro
O secretário de saúde comprará recipientes de um mesmo tipo, de modo a instalar 20 deles em cada escola, abastecidos com álcool em gel na sua capacidade máxima, de forma a utilizar todo o gel dos galões de uma só vez.
A maior piscina do mundo, registrada no livro Guiness, - ENEM 2014
MatemáticaA maior piscina do mundo, registrada no livro Guiness, está localizada no Chile, em San Alfonso del Mar, cobrindo um terreno de 8 hectares de área.
Sabe-se que 1 hectare corresponde a 1 hectômetro quadrado.
Os incas desenvolveram uma maneira de registrar - ENEM 2014
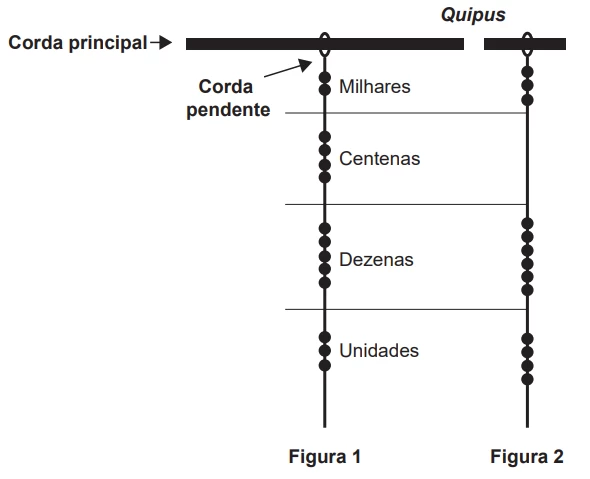
MatemáticaOs incas desenvolveram uma maneira de registrar quantidades e representar números utilizando um sistema de numeração decimal posicional: um conjunto de cordas com nós denominado quipus. O quipus era feito de uma corda matriz, ou principal (mais grossa que as demais), na qual eram penduradas outras cordas, mais finas, de diferentes tamanhos e cores (cordas pendentes). De acordo com a sua posição, os nós significavam unidades, dezenas, centenas e milhares. Na Figura 1, o quipus representa o número decimal 2 453. Para representar o “zero” em qualquer posição, não se coloca nenhum nó.
Um executivo sempre viaja entre as cidades A e B, que - ENEM 2014
MatemáticaUm executivo sempre viaja entre as cidades A e B, que estão localizadas em fusos horários distintos. O tempo de duração da viagem de avião entre as duas cidades é de 6 horas. Ele sempre pega um voo que sai de A às 15h e chega à cidade B às 18h (respectivos horários locais).
Certo dia, ao chegar à cidade B, soube que precisava estar de volta à cidade A, no máximo, até as 13h do dia seguinte (horário local de A).