Disciplina: Matemática 0 Curtidas
A região hachurada do plano cartesiano xOy contida no - FUVEST 2021
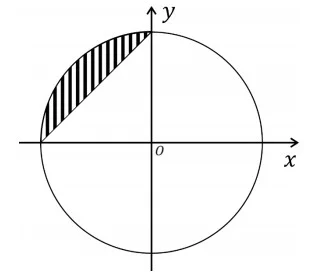
A região hachurada do plano cartesiano xOy contida no círculo de centro na origem O e raio 1, mostrada na figura, pode ser descrita por
-
{(x, y); x² + y² ≤ 1 e y – x ≤ 1}.
-
{(x, y); x² + y² ≥ 1 e y + x ≥ 1}.
-
{(x, y); x² + y² ≤ 1 e y – x ≥ 1}.
-
{(x, y); x² + y² ≤ 1 e y + x ≥ 1}.
-
{(x, y); x² + y² ≥ 1 e y + x ≤ 1}.
Solução
Alternativa Correta: C) {(x, y); x² + y² ≤ 1 e y – x ≥ 1}.
Nesta questão de geometria analítica, nós temos a limitação de uma área que é dada por uma equação de circunferência e uma equação de reta.
Equação da circunferência:
(x-0)² + (y-0)² = 1²
x² + y² = 1
Equação da reta:
Repare que a reta passa pelos pontos (-1,0) e (0,1). O coeficiente angular dessa reta é exatamente 1 e o ponto onde ela toca o eixo y também vale 1. Logo, a equação da reta é:
y = x + 1
Nosso objetivo é pegar o que está abaixo dessa equação de circunferência e o que está acima da equação de reta.
x² + y² ≤ 1 e y ≥ x+1 ajustando y-x ≥ 1
Finalmente queremos x² + y² ≤ 1 e y-x ≥ 1. Alternativa correta é a letra C.
Curiosidade: o ponto (10,10) faz parte dessa região? Não, pois nem chega a atender o primeiro critério 10² + 10² = 200 que não é menor nem igual a 1. Já o ponto (-0,8 ; 0,5) faz parte, pois:
(-0,8)² + (0,5)² = 0,64 + 0,25 = 0,89 que é menor ou igual a 1. Atendeu o 1º critério.
0,5 - (-0,8) = 0,5 + 0,8 = 1,3 que é maior ou igual a 1. Atendeu o 2º critério.
Créditos da Resolução: ER
Institução: FUVEST
Ano da Prova: 2021
Assuntos: Geometria Analítica, Equação de Círculo
Vídeo Sugerido: YouTube